1 序列模型
与序列相关的有趣概念
- 锚定(anchoring)效应:对于初始信息的过度重视,即常言道的”先入为主“
- 享乐适应(hedonic adaption):突然有钱比一直有钱更快乐,长期吃美食然后再吃普通的食物会觉得难吃,即常言道的”由奢入俭难“
序列预测的相关概念:
- 外推法(extrapolation):对超出已知观测范围进行预测
- 内插法(interpolation):在现有观测值之间进行估计
- 时间是向前推进的因果模型,正向估计通常比反向估计更容易
- 马尔可夫假设:当前数据只跟$\tau$个过去的数据相关,常用于简化模型
- $k$步预测:用前$n$天的数据预测第$n+1$天,再利用前$n-1$天和第$n+1$天结果预测第$n+2$天,直至第$n+k$天
- 对于$k$步预测,随着步数的增加,预测误差将会积累并放大
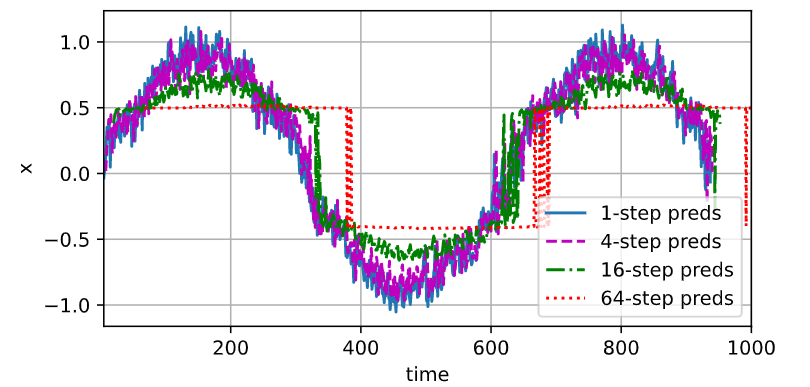
序列预测的基础方法:自回归、马尔可夫模型、隐变量模型
此处可参考[[1_study/algorithm/概率图类模型/隐马尔可夫模型 HMM]]
2 文本预处理
文本预处理的相关概念:
- 词元(token):文本的基本单位,每个词元都是一个字符串(string)
- 词表(vocabulary):将字符串类型的词元映射为数字索引
- 语料(corpus):训练集中的所有文档中的所有可能词元的汇总表
- 特殊词元:未知词元
<unk>、填充词元<pad>、 序列开始<bos>; 序列结束<eos>
3 语言模型和数据集
给定长度为$T$的文本序列${x-1,x_2,...,x_T}$,语言模型(language model)的目的是估计序列的联合概率:$P(x_1,x_2,...,x_T)$
以文本序列${deep,learning,is,fun}$为例,其序列的联合概率如下: $$P(deep)P(learning|deep)P(is|deep,learning)P(fun|deep,learning,is)$$ 其中的概率计算一般通过统计词频来实现近似估计: $$P(learning|deep)=\frac{n(deep,learning)}{n(deep)}$$ 当数据集很小或单词较为罕见时,可以考虑进行拉普拉斯平滑(Laplace smoothing),即对所有的计数都添加一个小常量
当文本序列很长时,联合概率的计算量会增加,同时也很容易出现$n(T)\leq1$的情况。此时可考虑引入马尔可夫假设简化计算:
- 一元语法(unigram):$p(x_1,x_2,x_3,x_4)=p(x_1)p(x_2)p(x_3)p(x_4)$
- 二元语法(bigram):$p(x_1,x_2,x_3,x_4)=p(x_1)p(x_2|x_1)p(x_3|x_2)p(x_4|x_3)$
- 三元语法(trigram):$p(x_1,x_2,x_3,x_4)=p(x_1)p(x_2|x_1)p(x_3|x_1,x_2)p(x_4|x_2,x_3)$
齐普夫定律(Zipf’s law):词频以一种明确的方式迅速衰减(排除部分离群点后,在双对数坐标图上表现为一条直线),假设第$i$个最常见的单词的词频$n_i$
$$logn_i=-\alpha log_i+c$$
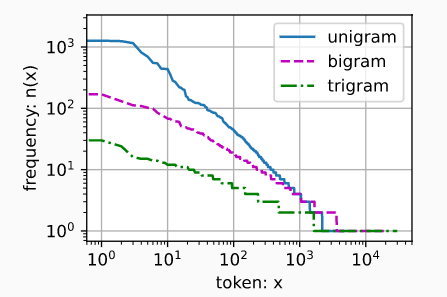
序列的采样
- 偏移量的随机:确保每次抽样的起始点不同,避免切割点的固化
- 随机采样(random sampling):相邻的随机子序列在原始序列上不一定是相邻的
- 顺序分区(sequential partitioning):相邻的随机子序列在原始序列上也是相邻的
基于PyTorch的序列采样实现
import random
import torch
from d2l import torch as d2l
def seq_data_iter_random(corpus, batch_size, num_steps): #@save
"""使用随机抽样生成一个小批量子序列"""
# 从随机偏移量开始对序列进行分区,随机范围包括num_steps-1
corpus = corpus[random.randint(0, num_steps - 1):]
# 减去1,是因为我们需要考虑标签
num_subseqs = (len(corpus) - 1) // num_steps
# 长度为num_steps的子序列的起始索引
initial_indices = list(range(0, num_subseqs * num_steps, num_steps))
# 在随机抽样的迭代过程中,
# 来自两个相邻的、随机的、小批量中的子序列不一定在原始序列上相邻
random.shuffle(initial_indices)
def data(pos):
# 返回从pos位置开始的长度为num_steps的序列
return corpus[pos: pos + num_steps]
num_batches = num_subseqs // batch_size
for i in range(0, batch_size * num_batches, batch_size):
# 在这里,initial_indices包含子序列的随机起始索引
initial_indices_per_batch = initial_indices[i: i + batch_size]
X = [data(j) for j in initial_indices_per_batch]
Y = [data(j + 1) for j in initial_indices_per_batch]
yield torch.tensor(X), torch.tensor(Y)
def seq_data_iter_sequential(corpus, batch_size, num_steps): #@save
"""使用顺序分区生成一个小批量子序列"""
# 从随机偏移量开始划分序列
offset = random.randint(0, num_steps)
num_tokens = ((len(corpus) - offset - 1) // batch_size) * batch_size
Xs = torch.tensor(corpus[offset: offset + num_tokens])
Ys = torch.tensor(corpus[offset + 1: offset + 1 + num_tokens])
Xs, Ys = Xs.reshape(batch_size, -1), Ys.reshape(batch_size, -1)
num_batches = Xs.shape[1] // num_steps
for i in range(0, num_steps * num_batches, num_steps):
X = Xs[:, i: i + num_steps]
Y = Ys[:, i: i + num_steps]
yield X, Y
# 原书中后续还有关于采样函数的后续封装,构建数据迭代器
4 循环神经网络
语言模型的评价指标1:平均交叉熵损失 $$\frac{1}{n}\Sigma_{t=1}^n=logP(x_t|x_{t-1},...,x_1)$$ 语言模型的评价指标1:困惑度(perplexity) $$exp(\frac{1}{n}\Sigma_{t=1}^n=logP(x_t|x_{t-1},...,x_1))$$
理解困惑度:下一个词元的实际选择数的调和平均数
- 当模型预测标签的准确率为1时(最好情况),模型的困惑度为1
- 当模型预测标签的准确率为0时(最差情况),模型的困惑度为正无穷大
- 当模型预测所有标签的概率相等时(baseline),模型的困惑度为词表长度
独热编码(one-hot encoding):将每个词元的数字索引映射为独立的单位向量
预热(warm-up):以较小的学习率训练模型,让模型找到更好的训练起始点(有点类似于参数初始化的优化),使得最终模型更稳健
对于长度为$T$的序列,RNN在正向传播中会迭代计算$T$个梯度,并在反向传播过程中产生长度为$O(T)$的矩阵乘法链(链式法则),导致数值不稳定。尤其是当$T$较大时,模型容易出现梯度爆炸或梯度消失的问题
梯度裁剪能有效预防梯度爆炸的问题。假设梯度为$g$,可以考虑采用以下方案进行梯度裁剪,约束梯度范式在$\theta$以内: $$g\leftarrow min(1,\frac{\theta}{||g||})g$$
此公式可理解为将梯度$g$投影到三维空间,并用半径为$\theta$的球对其进行裁剪
5 循环神经网络实现(pytorch)
5.1 从零开始版本
%matplotlib inline
import math
import torch
from torch import nn
from torch.nn import functional as F
from d2l import torch as d2l
batch_size, num_steps = 32, 35
# H.G.Wells的时光机器数据集
train\_iter, vocab = d2l.load_data_time_machine(batch_size, num_steps)
# 初始化RNN的模型参数
def get_params(vocab_size, num_hiddens, device):
num_inputs = num_outputs = vocab_size
def normal(shape):
return torch.randn(size=shape, device=device) * 0.01
# 隐藏层参数
W_xh = normal((num_inputs, num_hiddens))
W_hh = normal((num_hiddens, num_hiddens))
b_h = torch.zeros(num_hiddens, device=device)
# 输出层参数
W_hq = normal((num_hiddens, num_outputs))
b_q = torch.zeros(num_outputs, device=device)
# 附加梯度
params = [W_xh, W_hh, b_h, W_hq, b_q]
for param in params:
param.requires_grad_(True)
return params
# 隐变量的初始化:用0填充的张量
def init_rnn_state(batch_size, num_hiddens, device):
return (torch.zeros((batch_size, num_hiddens), device=device), )
# 定义隐藏层和输出层的计算 激活函数使用tanh
def rnn(inputs, state, params):
# inputs的形状:(时间步数量,批量大小,词表大小)
W_xh, W_hh, b_h, W_hq, b_q = params
H, = state
outputs = []
# X的形状:(批量大小,词表大小)
for X in inputs:
H = torch.tanh(torch.mm(X, W_xh) + torch.mm(H, W_hh) + b_h)
Y = torch.mm(H, W_hq) + b_q
outputs.append(Y)
return torch.cat(outputs, dim=0), (H,)
# RNN的类封装,输出(时间步数×批量大小,词表大小), 隐状态(批量大小,隐藏单元数)
class RNNModelScratch: #@save
"""从零开始实现的循环神经网络模型"""
def __init__(self, vocab_size, num_hiddens, device,
get_params, init_state, forward_fn):
self.vocab_size, self.num_hiddens = vocab_size, num_hiddens
self.params = get_params(vocab_size, num_hiddens, device)
self.init_state, self.forward_fn = init_state, forward_fn
def __call__(self, X, state):
X = F.one_hot(X.T, self.vocab_size).type(torch.float32)
return self.forward_fn(X, state, self.params)
def begin_state(self, batch_size, device):
return self.init_state(batch_size, self.num_hiddens, device)
# 预测:注意先借助warmup机制初始化隐变量
def predict_ch8(prefix, num_preds, net, vocab, device): #@save
"""在prefix后面生成新字符"""
state = net.begin_state(batch_size=1, device=device)
outputs = [vocab[prefix[0]]]
get_input = lambda: torch.tensor([outputs[-1]], device=device).reshape((1, 1))
for y in prefix[1:]: # 预热期
_, state = net(get_input(), state)
outputs.append(vocab[y])
for _ in range(num_preds): # 预测num_preds步
y, state = net(get_input(), state)
outputs.append(int(y.argmax(dim=1).reshape(1)))
return ''.join([vocab.idx_to_token[i] for i in outputs])
# 梯度裁剪
def grad_clipping(net, theta): #@save
"""裁剪梯度"""
if isinstance(net, nn.Module):
params = [p for p in net.parameters() if p.requires_grad]
else:
params = net.params
norm = torch.sqrt(sum(torch.sum((p.grad ** 2)) for p in params))
if norm > theta:
for param in params:
param.grad[:] *= theta / norm
#@save
def train_epoch_ch8(net, train\_iter, loss, updater, device, use_random_iter):
"""训练网络一个迭代周期(定义见第8章)"""
state, timer = None, d2l.Timer()
metric = d2l.Accumulator(2) # 训练损失之和,词元数量
for X, Y in train\_iter:
if state is None or use_random_iter:
# 在第一次迭代或使用随机抽样时初始化state
state = net.begin_state(batch_size=X.shape[0], device=device)
else:
if isinstance(net, nn.Module) and not isinstance(state, tuple):
# state对于nn.GRU是个张量
state.detach_()
else:
# state对于nn.LSTM或对于我们从零开始实现的模型是个张量
for s in state:
s.detach_()
y = Y.T.reshape(-1)
X, y = X.to(device), y.to(device)
y_hat, state = net(X, state)
l = loss(y_hat, y.long()).mean()
if isinstance(updater, torch.optim.Optimizer):
updater.zero_grad()
l.backward()
grad_clipping(net, 1)
updater.step()
else:
l.backward()
grad_clipping(net, 1)
# 因为已经调用了mean函数
updater(batch_size=1)
metric.add(l * y.numel(), y.numel())
return math.exp(metric[0] / metric[1]), metric[1] / timer.stop()
#@save
def train_ch8(net, train\_iter, vocab, lr, num_epochs, device,
use_random_iter=False): # 可选择随机抽样方法训练模型
"""训练模型(定义见第8章)"""
loss = nn.CrossEntropyLoss()
animator = d2l.Animator(xlabel='epoch', ylabel='perplexity',
legend=['train'], xlim=[10, num_epochs])
# 初始化
if isinstance(net, nn.Module):
updater = torch.optim.SGD(net.parameters(), lr)
else:
updater = lambda batch_size: d2l.sgd(net.params, lr, batch_size)
predict = lambda prefix: predict_ch8(prefix, 50, net, vocab, device)
# 训练和预测
for epoch in range(num_epochs):
ppl, speed = train_epoch_ch8(
net, train\_iter, loss, updater, device, use_random_iter)
if (epoch + 1) % 10 == 0:
print(predict('time traveller'))
animator.add(epoch + 1, [ppl])
print(f'困惑度 {ppl:.1f}, {speed:.1f} 词元/秒 {str(device)}')
print(predict('time traveller'))
print(predict('traveller'))
num_epochs, lr = 500, 1
train_ch8(net, train\_iter, vocab, lr, num_epochs, d2l.try_gpu())
# 困惑度 1.0, 76623.6 词元/秒 cuda:0
# time travelleryou can show black is white by argument said filby
# travelleryou can show black is white by argument said filby
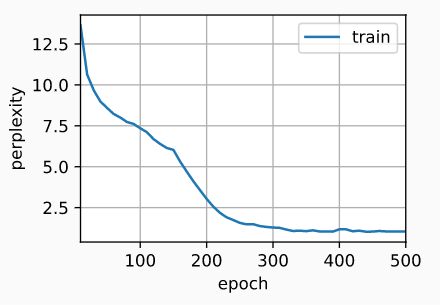
5.2 简洁实现版本
import torch
from torch import nn
from torch.nn import functional as F
from d2l import torch as d2l
batch_size, num_steps = 32, 35
train\_iter, vocab = d2l.load_data_time_machine(batch_size, num_steps)
num_hiddens = 256
# 初始化参数与隐状态
rnn_layer = nn.RNN(len(vocab), num_hiddens)
state = torch.zeros((1, batch_size, num_hiddens))
#@save
class RNNModel(nn.Module):
"""循环神经网络模型"""
def __init__(self, rnn_layer, vocab_size, **kwargs):
super(RNNModel, self).__init__(**kwargs)
self.rnn = rnn_layer
self.vocab_size = vocab_size
self.num_hiddens = self.rnn.hidden_size
# 如果RNN是双向的(之后将介绍),num_directions应该是2,否则应该是1
if not self.rnn.bidirectional:
self.num_directions = 1
self.linear = nn.Linear(self.num_hiddens, self.vocab_size)
else:
self.num_directions = 2
self.linear = nn.Linear(self.num_hiddens * 2, self.vocab_size)
def forward(self, inputs, state):
X = F.one_hot(inputs.T.long(), self.vocab_size)
X = X.to(torch.float32)
Y, state = self.rnn(X, state)
# 全连接层首先将Y的形状改为(时间步数*批量大小,隐藏单元数)
# 它的输出形状是(时间步数*批量大小,词表大小)。
output = self.linear(Y.reshape((-1, Y.shape[-1])))
return output, state
def begin_state(self, device, batch_size=1):
if not isinstance(self.rnn, nn.LSTM):
# nn.GRU以张量作为隐状态
return torch.zeros((self.num_directions * self.rnn.num_layers,
batch_size, self.num_hiddens),
device=device)
else:
# nn.LSTM以元组作为隐状态
return (torch.zeros((
self.num_directions * self.rnn.num_layers,
batch_size, self.num_hiddens), device=device),
torch.zeros((
self.num_directions * self.rnn.num_layers,
batch_size, self.num_hiddens), device=device))
# 训练预测
device = d2l.try_gpu()
net = RNNModel(rnn_layer, vocab_size=len(vocab))
net = net.to(device)
d2l.predict_ch8('time traveller', 10, net, vocab, device)
num_epochs, lr = 500, 1
d2l.train_ch8(net, train\_iter, vocab, lr, num_epochs, device)
# perplexity 1.3, 288387.8 tokens/sec on cuda:0
# time travellerit s against reason said filbycentalill cas ald it
# travelleredifte tr ars in the mert we cannet ee laig torep
6 循环神经网络实现(tensorflow)
6.1 从零开始版本
%matplotlib inline
import math
import tensorflow as tf
from d2l import tensorflow as d2l
batch_size, num_steps = 32, 35
train\_iter, vocab = d2l.load_data_time_machine(batch_size, num_steps)
# H.G.Wells的时光机器数据集
train_random_iter, vocab_random_iter = d2l.load_data_time_machine(
batch_size, num_steps, use_random_iter=True)
# 初始化RNN的模型参数
def get_params(vocab_size, num_hiddens):
num_inputs = num_outputs = vocab_size
def normal(shape):
return tf.random.normal(shape=shape,stddev=0.01,mean=0,dtype=tf.float32)
# 隐藏层参数
W_xh = tf.Variable(normal((num_inputs, num_hiddens)), dtype=tf.float32)
W_hh = tf.Variable(normal((num_hiddens, num_hiddens)), dtype=tf.float32)
b_h = tf.Variable(tf.zeros(num_hiddens), dtype=tf.float32)
# 输出层参数
W_hq = tf.Variable(normal((num_hiddens, num_outputs)), dtype=tf.float32)
b_q = tf.Variable(tf.zeros(num_outputs), dtype=tf.float32)
params = [W_xh, W_hh, b_h, W_hq, b_q]
return params
# 隐变量的初始化:用0填充的张量
def init_rnn_state(batch_size, num_hiddens):
return (tf.zeros((batch_size, num_hiddens)), )
# 定义隐藏层和输出层的计算 激活函数使用tanh
def rnn(inputs, state, params):
# inputs的形状:(时间步数量,批量大小,词表大小)
W_xh, W_hh, b_h, W_hq, b_q = params
H, = state
outputs = []
# X的形状:(批量大小,词表大小)
for X in inputs:
X = tf.reshape(X,[-1,W_xh.shape[0]])
H = tf.tanh(tf.matmul(X, W_xh) + tf.matmul(H, W_hh) + b_h)
Y = tf.matmul(H, W_hq) + b_q
outputs.append(Y)
return tf.concat(outputs, axis=0), (H,)
# RNN的类封装,输出(时间步数×批量大小,词表大小), 隐状态(批量大小,隐藏单元数)
class RNNModelScratch: #@save
"""从零开始实现的循环神经网络模型"""
def __init__(self, vocab_size, num_hiddens,
init_state, forward_fn, get_params):
self.vocab_size, self.num_hiddens = vocab_size, num_hiddens
self.init_state, self.forward_fn = init_state, forward_fn
self.trainable_variables = get_params(vocab_size, num_hiddens)
def __call__(self, X, state):
X = tf.one_hot(tf.transpose(X), self.vocab_size)
X = tf.cast(X, tf.float32)
return self.forward_fn(X, state, self.trainable_variables)
def begin_state(self, batch_size, *args, **kwargs):
return self.init_state(batch_size, self.num_hiddens)
# 预测:注意先借助warmup机制初始化隐变量
def predict_ch8(prefix, num_preds, net, vocab): #@save
"""在prefix后面生成新字符"""
state = net.begin_state(batch_size=1, dtype=tf.float32)
outputs = [vocab[prefix[0]]]
get_input = lambda: tf.reshape(tf.constant([outputs[-1]]),
(1, 1)).numpy()
for y in prefix[1:]: # 预热期
_, state = net(get_input(), state)
outputs.append(vocab[y])
for _ in range(num_preds): # 预测num_preds步
y, state = net(get_input(), state)
outputs.append(int(y.numpy().argmax(axis=1).reshape(1)))
return ''.join([vocab.idx_to_token[i] for i in outputs])
# 梯度裁剪
def grad_clipping(grads, theta): #@save
"""裁剪梯度"""
theta = tf.constant(theta, dtype=tf.float32)
new_grad = []
for grad in grads:
if isinstance(grad, tf.IndexedSlices):
new_grad.append(tf.convert_to_tensor(grad))
else:
new_grad.append(grad)
norm = tf.math.sqrt(sum((tf.reduce_sum(grad ** 2)).numpy()
for grad in new_grad))
norm = tf.cast(norm, tf.float32)
if tf.greater(norm, theta):
for i, grad in enumerate(new_grad):
new_grad[i] = grad * theta / norm
else:
new_grad = new_grad
return new_grad
#@save
def train_epoch_ch8(net, train\_iter, loss, updater, use_random_iter):
"""训练模型一个迭代周期(定义见第8章)"""
state, timer = None, d2l.Timer()
metric = d2l.Accumulator(2) # 训练损失之和,词元数量
for X, Y in train\_iter:
if state is None or use_random_iter:
# 在第一次迭代或使用随机抽样时初始化state
state = net.begin_state(batch_size=X.shape[0], dtype=tf.float32)
with tf.GradientTape(persistent=True) as g:
y_hat, state = net(X, state)
y = tf.reshape(tf.transpose(Y), (-1))
l = loss(y, y_hat)
params = net.trainable_variables
grads = g.gradient(l, params)
grads = grad_clipping(grads, 1)
updater.apply_gradients(zip(grads, params))
# Keras默认返回一个批量中的平均损失
metric.add(l * d2l.size(y), d2l.size(y))
return math.exp(metric[0] / metric[1]), metric[1] / timer.stop()
#@save
def train_ch8(net, train\_iter, vocab, lr, num_epochs, strategy,
use_random_iter=False): # 可选择随机抽样方法训练模型
"""训练模型(定义见第8章)"""
with strategy.scope():
loss = tf.keras.losses.SparseCategoricalCrossentropy(
from_logits=True)
updater = tf.keras.optimizers.SGD(lr)
animator = d2l.Animator(xlabel='epoch', ylabel='perplexity',
legend=['train'], xlim=[10, num_epochs])
predict = lambda prefix: predict_ch8(prefix, 50, net, vocab)
# 训练和预测
for epoch in range(num_epochs):
ppl, speed = train_epoch_ch8(net, train\_iter, loss, updater,
use_random_iter)
if (epoch + 1) % 10 == 0:
print(predict('time traveller'))
animator.add(epoch + 1, [ppl])
device = d2l.try_gpu()._device_name
print(f'困惑度 {ppl:.1f}, {speed:.1f} 词元/秒 {str(device)}')
print(predict('time traveller'))
print(predict('traveller'))
num_epochs, lr = 500, 1
train_ch8(net, train\_iter, vocab, lr, num_epochs, d2l.try_gpu())
# 困惑度 1.0, 9968.4 词元/秒 /GPU:0
# time travelleryou can show black is white by argument said filby
# traveller for so it will be convenient to speak of himwas e
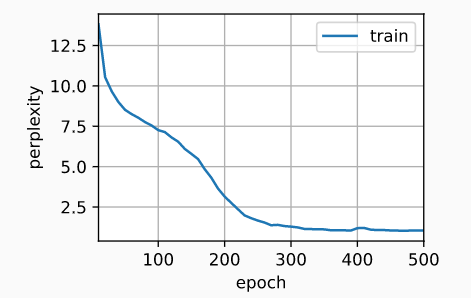
6.2 简洁实现版本
import tensorflow as tf
from d2l import tensorflow as d2l
batch_size, num_steps = 32, 35
train\_iter, vocab = d2l.load_data_time_machine(batch_size, num_steps)
num_hiddens = 256
# 初始化参数与隐状态
rnn_cell = tf.keras.layers.SimpleRNNCell(num_hiddens,
kernel_initializer='glorot_uniform')
rnn_layer = tf.keras.layers.RNN(rnn_cell, time_major=True,
return_sequences=True, return_state=True)
state = rnn_cell.get_initial_state(batch_size=batch_size, dtype=tf.float32)
state.shape
#@save
class RNNModel(tf.keras.layers.Layer):
def __init__(self, rnn_layer, vocab_size, **kwargs):
super(RNNModel, self).__init__(**kwargs)
self.rnn = rnn_layer
self.vocab_size = vocab_size
self.dense = tf.keras.layers.Dense(vocab_size)
def call(self, inputs, state):
X = tf.one_hot(tf.transpose(inputs), self.vocab_size)
# rnn返回两个以上的值
Y, *state = self.rnn(X, state)
output = self.dense(tf.reshape(Y, (-1, Y.shape[-1])))
return output, state
def begin_state(self, *args, **kwargs):
return self.rnn.cell.get_initial_state(*args, **kwargs)
# 训练与预测
device_name = d2l.try_gpu()._device_name
strategy = tf.distribute.OneDeviceStrategy(device_name)
with strategy.scope():
net = RNNModel(rnn_layer, vocab_size=len(vocab))
d2l.predict_ch8('time traveller', 10, net, vocab)
num_epochs, lr = 500, 1
d2l.train_ch8(net, train\_iter, vocab, lr, num_epochs, strategy)
# perplexity 1.4, 14418.1 tokens/sec on /GPU:0
# time traveller smiled arively o spact but ll opocancomment mark
# traveller the exome the tome tree goting an f me his it tis
7 通过时间反向传播
不同于普通神经网络的反向传播,RNN类网络不仅需要考虑梯度在不同层间的纵向传播,还要考虑梯度在不同时刻间的横向传播(BackPropogation Through Time,即BPTT),并在两个方向同时进行参数优化(核心依然是链式法则)。
考虑到过长的序列反向传播容易导致梯度不稳定的问题,还可以酌情进行梯度传播的裁剪,以提高效率和模型稳定性。RNN的常见反向传播策略:
- 完全计算。每次都计算完整的链式法则,计算成本高,容易导致模型不稳定
- 常规截断。每次反向传播仅递归$\tau$次,侧重于短期影响,使得最终模型简单而稳定
- 随机截断。次数$\tau$为随机变量,次数$\tau$越大(小概率事件),最终梯度的权重越高
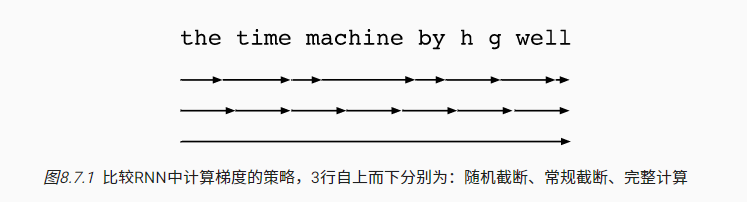
随机截断方法理论上很优秀,但实际表现并不比常规截断好
- 常规截断足以让模型捕获实际的依赖关系,有时并不需要关注长期影响
- 随机截断中的随机变量增加了模型的方差,抵消了长步数带来的额外收益
- 截断过程使得反向传播方法具备了轻度的正则化效果