HATR：基于分层自适应时间关系网络的股票预测
发表评论
515 views

中文标题：分层自适应时间关系建模的股票趋势预测

英文标题：Hierarchical Adaptive Temporal-Relational Modeling for Stock Trend Prediction

发布平台：IJCAI

IJCAI

发布日期：2021-08-01

引用量（非实时）：33

DOI：10.24963/ijcai.2021/508

作者：Heyuan Wang, Shun Li, Tengjiao Wang, Jiayi Zheng

关键字： #HATR #GCN

文章类型：conferencePaper

品读时间：2023-12-14 10:24

1 文章萃取

1.1 核心观点

本文提出了一种新颖的分层自适应时间关系网络（HATR）来表征和预测股票演化。HATR 通过堆叠膨胀因果卷积和门控路径，从股票交易时序的多尺度局部组合中逐渐掌握短期和长期转换特点；本文还提出了基于霍克斯过程和特定目标查询的双重注意机制，以检测重要的时间点和尺度来深化对于股票特征的表达
此外，本文还提出了基于GCN的多图交互模块，该模块中的图构建既包含了历史的领域知识，也有基于数据驱动的自适应学习，并捕获到了股票之间的相互依赖性
最终， HATR 通过端到端框架训练，在三个真实世界股票市场数据集，展现出了超过其他模型的性能表现，并通过消融实验和注意力可视化进行了更深层的模型分析

1.2 综合评价

  • HATR 通过端到端框架，实现了时间和尺度层面的信息抽取
  • HATR 多图交互模块也很好地平衡了领域知识和自适应能力
  • 综合性很强，实验分析也很详细；最终回测性能有点低于预期

1.3 主观评分：⭐⭐⭐⭐⭐

2 精读笔记

HATR（Hierarchical Adaptive Temporal-Relational Network）由两个主要模块组成，即根据历史波动率构建股票表示的时间模块，和根据学习到的节点特征矩阵捕获股票间依赖性的关系模块

2.1 多尺度时间表示

前置知识：膨胀卷积、因果卷积

前置知识：霍克斯过程（Hawkes Process）

  • 一种用于建模自激励（self-exciting）过程的数学模型，是基本泊松过程的扩展
  • 霍克斯过程是一个描述随着时间发生的一系列事件的计数过程，每一件事件的发生都会增加（激励）下一件事情发生的可能性，同时这个激励的效果会随着时间衰减
  • 霍克斯过程常用于金融、流行病学、地震学等；下图展示了一个简单的霍克斯过程：

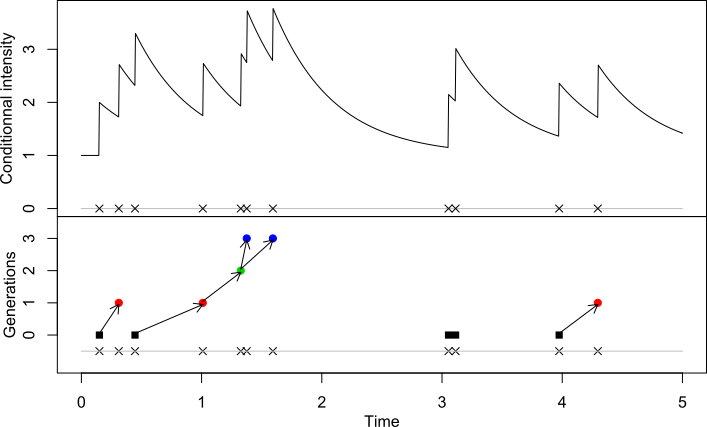
多尺度时间表示模型结构如下：

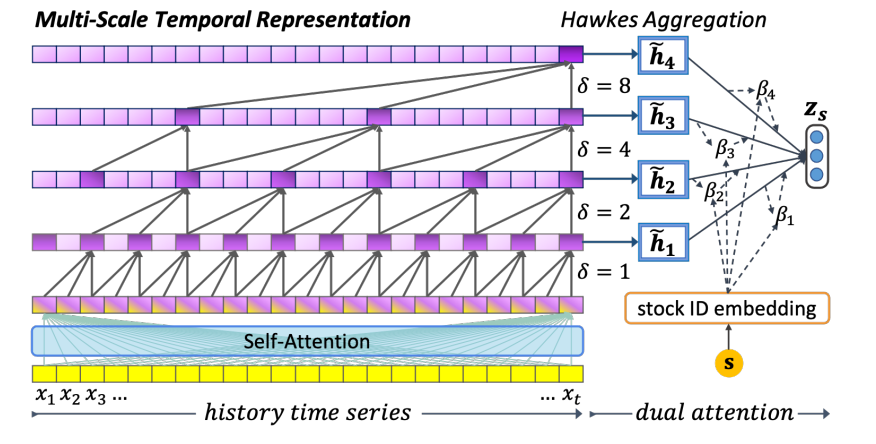
  • 该模块的输入为给定股票的历史价格时序数据，输出为给定股票的嵌入表示
  • 数据首先经过自注意力层和残差连接得到初步抽取的股票时序特征$\mathcal{X}_i=\mathcal{X}_i+Att(i)$，之后经过带有门控线性单元（GLU）的因果膨胀卷积实现信息流的有效分层： $$\mathrm{GLU}(\mathcal{X}_k)=\left(\boldsymbol{\Theta}_1\\mathcal{X}_k+\boldsymbol{b}_1\right)\odot\sigma(\boldsymbol{\Theta}_2\\mathcal{X}_k+\boldsymbol{b}_2),$$

上式中，$\boldsymbol{\Theta}$表示一组卷积核；$*$表示因果膨胀卷积运算；$\sigma$表示控制信息传输的 sigmoid 函数

  • 定义第$l$层的$GLU$特征输出为$h^{(l)}$，本文采用霍克斯过程来按时间依次聚合每个编码层的顺序特征。其中第$l$层时间步$k$的特征权重为（指数级衰减）： $$\lambda_{k}(l;\theta)=\frac{\exp(\boldsymbol{h}_{k}^{(l)T}\boldsymbol{W}\boldsymbol{h}_{t}^{(l)})}{\sum_{\mathrm{i}}\exp{(\boldsymbol{h}_{\mathrm{i}}^{(l)T}\boldsymbol{W}\boldsymbol{h}_{t}^{(l)})}}\times\left(1+\epsilon\exp(-\gamma\Delta t_{k})\right)$$
  • 加权聚合后的特征 $\tilde{\boldsymbol{h}}_l=\sum_k\lambda_k(l;\theta)\boldsymbol{h}_k^{(l)}$ 会再通过一种特定于目标的注意力机制来识别不同时间尺度的重要性；随着深度的增加（从$\tilde{\boldsymbol{h}}_1$到$\tilde{\boldsymbol{h}}_4$），聚合特征对应的时间尺度也在逐渐放宽

由于个股的波动幅度和频率不同，不同长短期尺度的转变规律也表现出不同的影响

  • 假设股票$s$的第$l$层聚合特征$\tilde{\boldsymbol{h}}_l$对应的注意力权重为$\beta_l$，其计算公式如下： $$\begin{aligned}

&\boldsymbol{q}_s=ReLU(\mathbf{V}_d\times\boldsymbol{e}_s+\boldsymbol{b}_d) \\ &\bar{h} {}_l^{'}=tanh(\mathbf{V}_q\bar{\boldsymbol{h}}_l+\boldsymbol{b}_q) \\ &\beta_{l} =\frac{\exp(\boldsymbol{q}_s^T\bar{\boldsymbol{h}}_l^{\prime})}{\sum_{j=1}^L\exp(\boldsymbol{q}_s^T\bar{\boldsymbol{h}}_j^{\prime})} \end{aligned}$$

上式中，$q_s$和$\bar{h} {}_l^{'}$分别表示特定目标注意力机制的query和key；$V_d$表示股票id构成的one-hot向量，$e_s$表示可训练的参数（在[-0.1,0.1]范围内进行随机初始化），因此$q_s$得到的是针对股票s的特定query，其计算方式等价于一个普通的嵌入层表示；

$V_q$是key的可训练参数；$b_d$和$b_q$也是可训练参数（截距项）

  • 最终的股票表示$\boldsymbol{z}=\sum_{l=1}^L\beta_l\tilde{\boldsymbol{h}}_l$将同时包含股票价格时序中的时间和尺度信息

2.2 股票相互关系模型

前置知识：GCN_基于图卷积网络的半监督学习

图卷积的核心思想是利用边的信息对节点信息进行聚合从而生成新的节点表示

关系图构建的核心是评估不同股票之间的关系（即，构建邻接矩阵$A$）

三种关系图的构建：

  1. 行业图（Industry Graph）：由于行业上下游关系，某些行业股票在回报变化上可能系统地领先或落后于其他行业股票，尤其是行业龙头企业；因此对于处于同一行业的两只股票：股票$i$和股票$j$，本文使用注册资本$C$和营业额$T$来构建二者之间的关系： $$a_{ij}=\frac{C_j}{C_i}+\frac{T_j}{T_i}$$
  2. 话题图（Topicality Graph）：根据网络信息来挖掘上市公司之间隐藏的话题性关联；本文使用金融词典来发现具有稳定相关（高共现）的看涨/看跌的股票对；股票对间的权重为相关话题的数量
  3. 自适应图（Self-Adaptive Graph）：为了填补基于规则构建图的局限性，本文提出了一种自适应的图构建方法；引入两个额外的嵌入字典$\boldsymbol{E}_{n1},\boldsymbol{E}_{n2}$，其中包含每个股票id的嵌入表示；每个嵌入表示都随机初始化后伴随模型训练过程自适应更新，最终的邻接矩阵计算如下： $$\mathcal{A}_{apt}=softmax(ReLU(\boldsymbol{E}_{n1}\boldsymbol{E}_{n2}^T))$$

股票相互关系模型结构如下：

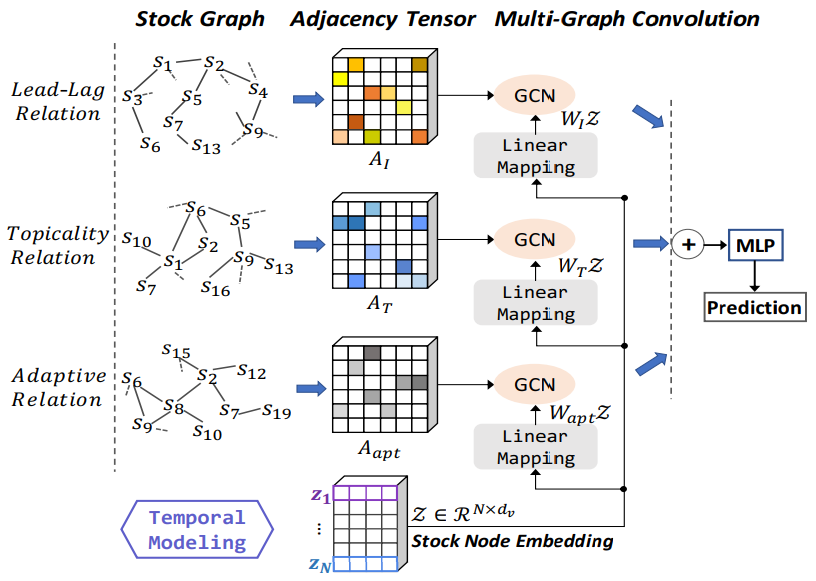
  • 将上一节得到的所有股票的表示$Z$作为图的节点表示，分别融合三种图的权重信息（邻接矩阵）后经过 GCN 模型处理，将知识图的信息融入到股票表示中
  • 最终三个 GCN 图模型输出的股票表示拼接后，直接预测股票趋势（上涨/下跌）

虽然中间包含很多模块，但HATR 的整体架构依然是端到端的二分类模型

2.3 实验结果和分析

实验设计说明：

  • 考虑了三种经典指数中的股票：沪深300指数、标普500指数、东证指数
  • 股票信息（开盘价/最高价/最低价/收盘价/交易量）、行业信息和资金数据来自 Wind；话题图构建所使用的网络文本来自雪球论坛和 0_life/精品资源/数据资源/知识图数据资源#Wikidata
  • 评价指标为 ACC、AUC、F1 分数和马修斯相关系数 （MCC）

数据和知识图说明：

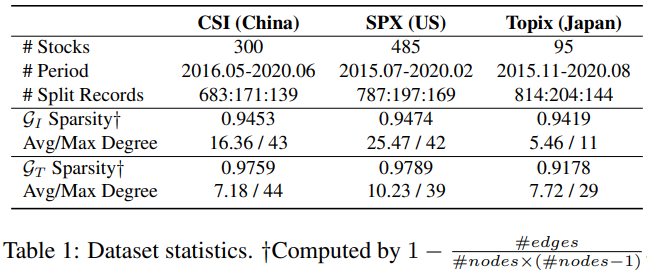
  • 当图中的节点全都连接时，图的稀疏度（Sparsity）为 0
  • 度（Degree）表示与该顶点关联的边的条数

不同模型的表现对比：

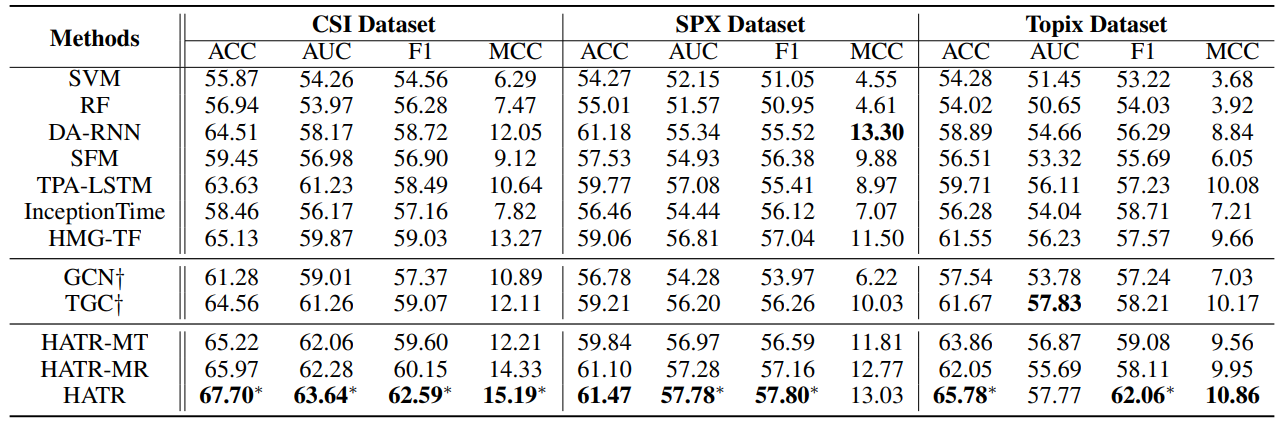
  • 基于神经的方法（例如DA-RNN、HMG-TF、TGC）通常优于传统的机器学习模型
  • 利用股票的相互关系通常可以对个体趋势预测产生积极的影响（GCN）
  • 相比于其他模型，本文提出 HATR 模型对应的大多数评价指标都有显着的优势
  • HATR-MT 和 HATR-MR 都存在性能下降，这表明时间模块和关系模块的综合贡献

部分模型说明：

  • DA-RNN [Qin et al., 2017] 使用具有注意机制的 LSTM 提取驱动输入和相关状态
  • TPA-LSTM [Shih et al., 2018] 通过结合注意力 LSTM 和卷积运算，将股票动态的时序不变特征转换到频域中
  • HMG-TF [Ding et al., 2020] 使用高斯先验和交易闭市区分，增强了 Transformer 的编码器性能，并针对每只股票的顺序数据进行建模
  • GCN [Kipf and Welling, 2017] 将时间序列数据作为节点的输入构建 GCN
  • TGC [Feng et al., 2019] 使用 LSTM 对股票编码，并将最后的状态提供给 GCN
  • HATR-MT 在 HATR 的基础上，删减了多尺度时间表示（改为普通 LSTM）
  • HATR-MR 是 HATR 的基础上，删减了捕获股票相互依赖性的多图关系模块

消融实验：

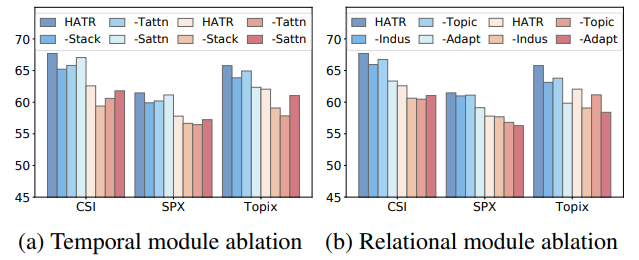
  • 蓝色和红色分别代表 ACC 和 F1 的评价结果
  • -Stack表示去除堆叠编码层（影响程度大）；-Tattn表示去除霍克斯过程（影响程度中）；-Satten表示去除尺度注意力（影响程度小）
  • -Indus表示去除行业图（影响程度中）；-Topic表示去除话题图（影响程度小）；-Adapt表示去除自适应图（影响程度大）

时间和尺度双重注意力分布的可视化：

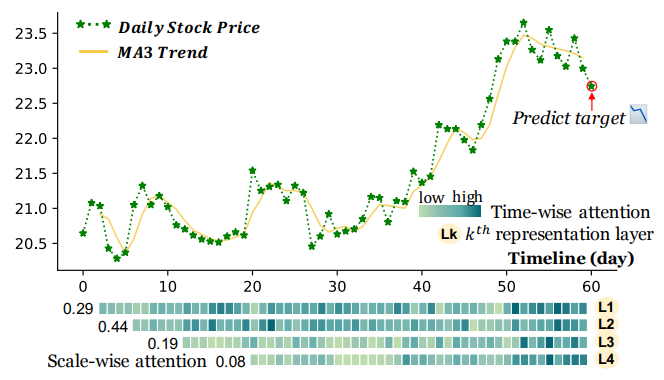
  • 较低的嵌入层捕获短期动态模式，较高的嵌入层用于检测长期趋势
  • 第 2 层的聚合特征注意力权重最高，第 4 层的聚合特征注意力权重最低
  • 股票价格近期的明显周期性规律变化通过霍克斯过程受到了更多关注

其他实验细节：

  • 编码维度在20~40之间更合适，过高和过低都会影响性能
  • 对于图的邻接矩阵，只考虑 2 步最合适；过高时性能明显下滑
  • 增大堆叠编码的层数时应该减少膨胀稀疏度；反之亦然

相关资源

往年同期文章