1 多模型融合的优势
Why it helps to combine models
模型的偏差与方差:
- 对于回归模型来说,预测的平方误差可以分解为偏差和方差
- 当模型过于简单时,预测精度低,此时模型的偏差过大
- 当模型过于复杂时,模型缺少泛化能力,模型方差过大
- 多个偏差大的简单模型通过融合后可以提高最终的预测精度(降低偏差)
- 多个过拟合(高方差)的模型融合后可以提高模型的稳定性(降低方差)
当单模型间的差异性(不是指性能差异)越大时,融合模型的效果越好
为什么模型融合会降低方差:
- 假设所有模型的预测均值为$\overline{y}$:
$$\overline{y}=\frac{1}{N}\Sigma_{i=1}^N y_i$$
- 假设真实值为$t$,则单模型对应的平方误差可表示如下:
$$\begin{align} \frac{1}{N}\sum_{i=1}^N(t-y_i)^2 &= \frac{1}{N}\sum_{i=1}^N\left((t-\bar{y}) - (y_i - \bar{y})\right)^2 \\ &= \frac{1}{N}\sum_{i=1}^N\left((t-\bar{y})^2 + (y_i - \bar{y})^2 - 2(t-\bar{y})(y_i-\bar{y})\right) \\ &= (t-\bar{y})^2 + \frac{1}{N}\sum_{i=1}^N(y_i-\bar{y})^2 - 2(t-\bar{y})\frac{1}{N}\sum_{i=1}^N(y_i - \bar{y}) \end{align}$$
- 假设不同模型间的预测是独立的,则上式右侧的第三项为0;第二项描述的是单模型的方差期望;第一项描述的是综合模型的平方误差
- 由此可知,由于单模型的方差大于0,因此综合模型的平方误差总是小于单模型的
再从贝叶斯解释的角度说明”模型融合会降低方差“
- 假设有两个模型,一个对正确标签给出的概率是$p_i$,另一个是$p_j$
- 从贝叶斯的角度,模型训练是为了追求预测正确标签的概率对数值最大
- 所以根据对数函数的性质可得,综合模型是优于随机的单个模型
$$\log(\frac{p_i+p_j}{2})\geq \frac{\log p_i+\log p_j}{2}$$
三个臭皮匠,顶个诸葛亮;但前提是三个臭皮匠各有所长
所以如何让模型能各有所长,是模型融合成功的关键
- 比如使用不同类型的建模方法(决策树,SVM,神经网络),再进行融合
- 如果仅使用神经网络算法,也可以设置不同的隐藏层、激活函数、超参
- 通过抽样等方式确保训练数据差异也是一种不错的方法,最常见的是Bagging算法和Boosting算法,具体可参阅集成算法一文
2 专家混合模型
Mixtures of Experts
核心思想:把数据集看作是来自不同领域信息的组合,通过设定不同的数据权重来训练多个神经网络,每个网络只专精特定领域的数据子集,实现单模型的各有所长
MoE会导致数据碎片化,在小数据集上效果不好,更适用于数据量较多的场景
局部模型(local model) VS 全局模型(global model)
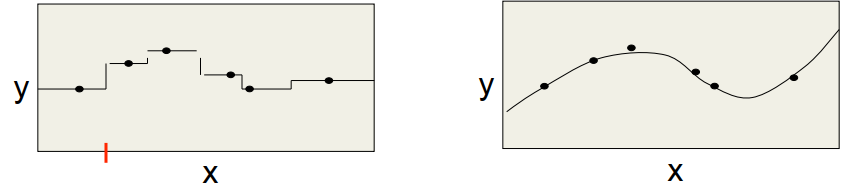
- 局部模型一般训练较快,预测输出分布不平滑;典型的局部模型如K近邻算法,保留所有样本并且不需要训练,根据与输入最相似的K个已知样本指导预测
- 全局模型一般训练较慢并且不稳定,容易受到数据微小变动的影响,但预测输出分布平滑;典型的全局模型如多项式回归,根据训练集拟合求解多项式函数的参数