本节课介绍了处理模型过拟合的常见方法(正则化项、惩罚因子),并展示了基于贝叶斯解读的一种实践有效的惩罚因子调参方法。
1 回顾过拟合
Reminder:Overfitting
训练数据中不仅蕴含着正确的规律/知识值得学习,也会存在偶然的错误(采样误差),而当模型学习到这类错误时就会出现泛化能力的下降——过拟合
如何防止过拟合:
- 更多的数据(算力充足情况下的最优解,力大飞砖!)
- 选择合适复杂度的模型(拟合到真实的规律,忽略偶然的错误)
- 融合多种类型的模型(三个臭皮匠,顶个诸葛亮)
- 贝叶斯方法,融合同一神经网络在不同的参数值下的预测结果(详见第4小节)
如何选择合适复杂度的模型(方法2)
- 网络架构:限制隐藏层数据或每层的神经元数,实现对参数量的控制
- 早停(Early stopping):初始参数值较小,并在过拟合前停止训练
- 正则项惩罚:通过L1或L2正则来惩罚过大的权重,约束模型复杂度
- 噪音:在参数值或激活函数中添加噪声(类似于数据增强),提高模型鲁棒性
1.1 超参选择与交叉验证
可能的超参:隐藏层单元数、正则项系数等
超参选择方法:交叉验证
- 将数据集拆分为三个子集:训练集、验证集、测试集
- 训练集用来训练模型,验证集用来指导超参的选择
- 测试集用来评估最终的模型表现(一般性能表现略低于验证集)
K折交叉验证:
- 划分出测试集后,将剩余数据划分为K份
- 每次使用其中的K-1份训练,用剩下的第K份验证
- 轮换训练K次后,得到关于超参的K次估计结果
1.2 早停(Early stopping)
早停,提前停止法(Early stopping):使用较小的参数值对模型进行初始化,之后训练更新模型并定期使用验证集检验模型效果,在效果变差时停止训练
当模型在验证集的效果达到最大时,模型最有可能学习到必然规律;而当模型在验证集上的性能开始下降时,则说明模型可能在学习不必要的偶然错误
问:为什么参数值小,模型的复杂度低?
答:当参数值很小的时候,对logistic函数来讲,输入接近0,则输出将恰好处于其线性的部分,所以整个网络都是接近线性的。从另一个角度来说,参数值接近0也限制了模型的整体参数量
2 限制参数的大小
Limiting the size of the weights
2.1 正则项惩罚
假设误差函数为E,则添加L2正则项的成本函数C可表示如下: $$C=E+\frac{\lambda}{2}\Sigma_i w_i^2$$ 对$w_i$求偏导可得: $$\frac{\partial{C}}{\partial{w_i}}=\frac{\partial{E}}{\partial{w_i}}+\lambda w_i$$ 令$\frac{\partial{C}}{\partial{w_i}}=0$,可得此时的$w_i=-\frac{1}{\lambda}\frac{\partial{E}}{\partial{w_i}}$
所以L2正则通过向误差函数添加一个额外项来惩罚过大的参数值,当成本函数C处于最小值时($\frac{\partial{C}}{\partial{w_i}}=0$),除非误差导数$\frac{\partial{E}}{\partial{w_i}}$相对较大,否则参数$w_i$会保持较小参数值,从而避免模型出现无效的高值参数。
L2正则项的好处:
- 避免网络使用不必要的权重来拟合“偶然误差”,增强模型的泛化能力
- 参数值较小,此时logistic函数输出变化比输入小,模型更加“平稳”
- 对于两个相似的输入,具备正则项的神经元会更趋于权重均衡,而不是顾此失彼
相比于L2,L1正则项的惩罚会更激进(椭圆形函数图像 VS “V”字形函数图像),L1正则项会强制权重的绝对值尽量小,更容易减少/淘汰参数量
2.2 权重限制
除了成本惩罚,还可以对权重进行限制:
- 尽量避免权重值的范数(平方和)超过设定上限
- 惩罚效果由梯度(更新量)最大值绝对,不需要将所有权重都推向0
3 使用噪音作为正则项
Using noise as a regularizer
对输入添加高斯噪声,即输入变为$x_i+N(0,\sigma^2_i)$,经由权重$w_i$放大后,最终 的输出也会带有高斯噪声,即输出变为$y_j+N(0,w^2_i \sigma^2_i)$
当模型训练时最小化成本函数(平方误差)时,也会最小化$N(0,w^2_i \sigma^2_i)$这一项,因此高斯噪声的添加可以看作为权重$w_i$增加了一个系数为$\sigma^2$的L2正则项
关于高斯噪声等价于系数为$\sigma^2$的L2正则项证明,可参见下图:

对于更复杂的网络,也可以添加高斯噪声的方式来限制网络的能力。此时这种做法不再等价于使用L2惩罚项,但效果依然出色,尤其是针对RNN这类模型
激活函数也可以添加噪声(正向传播时随机输出0/1,但反向传播依然用真实值),但这种方法在训练集会导致模型效果变差,训练速度变慢;在测试集上则有一定的效果
4 贝叶斯方法
Introduction to the Bayesian Approach
贝叶斯方法考虑所有可能的超参数组合及生成给定数据集的概率
4.1 贝叶斯框架
贝叶斯框架:
- 所有的事物都存在先验分布(这一先验分布可能是模糊的)
- 根据真实/观测数据,综合先验分布和似然估计项得到后验分布
- 似然估计项可以根据给定的超参组合,生成对应观测数据的概率分布
- 当数据充足时,似然估计项便足够准确,并逐渐接近真实的概率分布
在数据充足的情况下,似然估计能够“克服”先验分布的局限性/模糊性
抛硬币-举例说明:
- 抛硬币的结果是随机独立事件,正面概率为p,反面概率为1-p
- 因此对于抛硬币的建模,只包含一个需求求解的参数:p
- 在投掷100次后,正面出现的次数为53,因此可得p=0.53
- 用贝叶斯框架思考,此时对应的似然估计项为$P(D)=p^{53}(1-p)^{47}$
- 通过最大似然估计($dP(D)/dp=0$)求解可得,p=0.53
4.2 参数的概率分布
最大似然法会选择超参p的值为0.53,但可能p=0.5才是更合理的选择;为了避免对单一答案的接受或拒绝,可以考虑参数p的所有可能取值并借助贝叶斯定理求解概率分布:
- 先验分布假设参数W的不同取值概率是相同的
- 根据观察到的数据D,可推测参数W的后验概率:
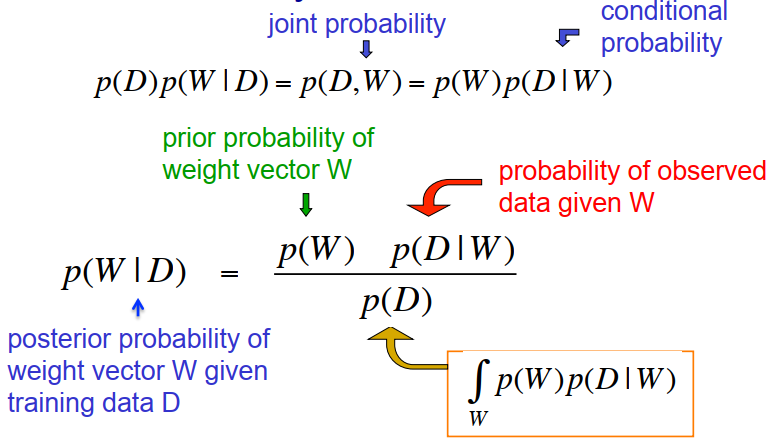
- 参数W给定数据D的后验分布,等于W的先验分布与给定W条件下观察到数据D的概率的乘积,最终再使用P(D)进行归一化;由于P(D)不依赖于W,因此有时可忽略。
5 用贝叶斯解释正则项惩罚
使用正则项惩罚手段模型的训练,就是在试图找出一组超参,能够同时满足关于参数值W的先验知识与数据集D的后验概率分布。这种方法也被称为最大后验估计(Maximum A Posteriori, MAP)
5.1 MLE 最大似然估计
假设模型预测值为$y$,真实值$t$可看作来自预测值+高斯噪声分布的结果: $$p(t_c|y_c)=\frac{1}{\sqrt{2\pi }\sigma}exp{-\frac{(t_c-y_c)^2}{2\sigma^2}}$$ 等式两边取对数,可得结果: $$-\log p(t_c|y_c)=k+\frac{(t_c-y_c)^2}{2\sigma^2},k=\frac{1}{\sqrt{2\pi }\sigma}$$ 等式左侧可看作代价/成本函数,其描述了真实值在给定预测值条件下的概率负对数(负的最大似然估计);右侧可看作真实值和预测值间的距离平方和,只不过有额外的系数和常数项
一般模型的训练过程是在不断追求成本/代价函数的最小化,也就是预测准确的概率(似然估计)最大化,也是预测误差(距离平方和)最小化
5.2 MAP 最大后验估计
由于神经网络涉及的参数量较多,所以很难使用贝叶斯方法直接估计所有参数值的后验分布;一种可行的方式是直接使用蒙特卡洛法模拟(Monte Carlo)法对正则项系数进行深入理解
本小节则通过构建以下几点假设,借助MAP算法对建模过程进行定性分析:
- 假设模型参数为$W$,对应的可观测数据(训练集)为$D$
- 假设不同样例间(比如输入为第$c$个样本$input_c$)是iid(独立同分布)
- 假设不同参数间(比如第$i$个参数是$w_i$)是iid(独立同分布)
- 假设参数值$w$服从均值为$w$,标准差为$\sigma_W$的正态分布
- 真实值$t$存在噪音,噪音满足均值为$0$,标准差为$\sigma_D$的正态分布
上文已证明高斯噪声等价于L2正则项,因此假设5其实是为了添加对正则项的实验分析
由假设1和假设2可知: $$p(D|W)=\prod_cp(t_c|W)=\prod_cp(t_c|f(input_c,W))=\prod_cp(t_c|y_c)$$ 等式两边取对数,可得结果: $$\log p(D|W)=\Sigma_c\log p(t_c|W)=\Sigma_c\log p(t_c|y_c)$$ 定义MAP的代价/成本函数为$-\log p(W|D)$,借助贝叶斯定理可得: $$-\log p(W|D)=-\log p(W)-\log p(D|W)+\log p(D)$$ 通过假设3和假设4可知上式右侧第一项中概率密度$p(w)$为: $$p(w)=\frac{1}{\sqrt{2\pi }\sigma}exp{-\frac{w^2}{2\sigma_W^2}} \Rightarrow -\log p(W)=-\Sigma_i \log p(w_i)=k+\Sigma_i\frac{w_i^2}{2\sigma_W^2}$$ 根据假设5以及上文已有的公式,对公式中第二项进行转化: $$-\log p(D|W)=-\Sigma_c\log p(t_c|y_c)=\Sigma_c\frac{(t_c-y_c)^2}{2\sigma_D^2}$$ 公式第三项与$W$无关,可忽略;最终MAP的代价/成本函数可简化为: $$C^{\ast}=\frac{1}{2\sigma_D^2}\Sigma_c(t_c-y_c)^2+\frac{1}{2\sigma_W^2}\Sigma_iw_i^2$$ 两边同时乘以$2\sigma^2_D$,可得: $$C=\Sigma_c(t_c-y_c)^2+\frac{2\sigma_D^2}{2\sigma_W^2}\Sigma_iw_i^2=E+\frac{2\sigma_D^2}{2\sigma_W^2}\Sigma_iw_i^2$$ 最终结果的$E$表示神经网络常用的误差函数(平方误差),而第二项则表示正则项惩罚,其中的正则项系数为$\frac{2\sigma_D^2}{2\sigma_W^2}$,此时系数不再是超参,而是可以确定的值
原本的超参需要根据交叉验证集反复尝试才能得到,但那只是类似于蒙特卡洛模拟的无奈之举;在理解了MAP的原理后,可以发现正则项系数其实不是人为设定的超参数,而是具备合理的高斯解释:即两个分布(参数分布 VS 真实值的噪音分布)的方差比
最大后验估计(MAP)在最大似然估计(Maximum Likelihood Estimate,MLE)的基础上考虑到了估计值$w$的先验分布;从最终结果来看,也可以看作是添加正则项后的最大似然估计
6 MacKay法设定正则项惩罚
早在1990s MacKay就根据正则项的贝叶斯解释,提出了一种设定正则的方法:
- 该方法不需要验证集,也不需要使用启发式方法搜寻最佳超参
- MacKay法首先随机初始化参数先验分布的方差和噪声分布方差,将两个方差的比值作为正则项的系数,然后训练模型并更新参数
- 将训练结果的残差方差设为噪声分布的方差,再根据训练后参数的实际分布估计参数方差;根据两个方差的比值得到新的正则项系数;
- 最后重复以上步骤,直到训练后参数满足零均值高斯分布
这一技巧被称为”empirical Bayes“,原理无法解释,但实践效果很不错