AlphaChip：用于布局规划的快速芯片设计

中文标题：用于布局规划的快速芯片设计
英文标题：A graph placement methodology for fast chip design
发布平台：Nature
发布日期：2021-06-10
引用量（非实时）：603
相关资源

中文标题：用于布局规划的快速芯片设计

英文标题：A graph placement methodology for fast chip design

发布平台：Nature

发布日期：2021-06-10

引用量（非实时）：603

DOI：10.1038/s41586-021-03544-w

作者：Azalia Mirhoseini, Anna Goldie, Mustafa Yazgan, Joe Wenjie Jiang, Ebrahim Songhori, Shen Wang, Young-Joon Lee, Eric Johnson, Omkar Pathak, Azade Nova, Jiwoo Pak, Andy Tong, Kavya Srinivasa, William Hang, Emre Tuncer, Quoc V. Le, James Laudon, Richard Ho, Roger Carpenter, Jeff Dean

关键字： #强化学习 #芯片设计

文章类型：journalArticle

品读时间：2024-11-14 18:21

1 文章萃取

1.1 核心观点

本文提出了一种基于强化学习的快速芯片设计方案；其中价值网络使用已标注进行有监督学习，策略网络则先借助价值网络的主干部分对输入关键信息进行嵌入表示，然后使用 PPO 算法根据完成芯片设计方案的奖励反馈进行参数更新。奖励函数的设计则依赖于传统的芯片性能评价指标。

在实验分析阶段，AlphaChip 体现出了超越传统算法和人类专家的芯片设计能力，并且对训练时未见过的芯片设计也具有较好的适用性。AlphaChip 在后续的现实实践中也逐步证明了自己的独特价值。

1.2 综合评价

整体的实现偏传统 RL，但对于芯片领域具备开创性

网络架构以 CNN 为核心，存在预测性能改善的空间

不适用于类型较多的标准单元，需要与传统算法配合

1.3 主观评分：⭐⭐⭐⭐⭐

2 精读笔记

2.1 背景知识

前置知识：芯片入门

芯片的层次化结构（由粗到细）：

基本模块，芯片中的高层次功能单元，包括存储子系统、计算单元或控制逻辑系统等
电路组件，构成模块的基本单元，包括宏（Macro）和标准单元
宏（Macro），预先设计和验证的较大功能块（包含多个标准单元和其他电路组件），通常用于实现复杂的功能。例如，存储器组件（如SRAM、ROM）
标准单元，实现基本逻辑功能的最小电路单元，例如逻辑门（NAND、NOR、XOR）、触发器、寄存器等

芯片设计相关的前置概念：

网表（Netlist）的含义：一个描述电路连接关系的列表，列出了所有模块的实例化信息（元件实例 Instances）和它们之间的连接（网络 Nets）。它是芯片设计的基础数据结构
电路组件的超图：超图 Hypergraph 是一种图的扩展，用于表示电路中多个节点之间的连接关系。每个节点代表一个电路组件（如宏或标准单元），边表示它们之间的连接
DRC（Design Rule Check），确保布局和布线网表符合流片要求的规则

芯片平面布局规划：

规划在芯片画布（二维网格）上进行，每个网格单元可以放置一个或多个电路组件
性能指标：功耗、延迟、面积（芯片的物理尺寸）和线长（影响功耗和延迟）
硬性约束：组件密度（避免过于集中或稀疏），拥挤度（避免布线困难或信号干扰）

AlphaChip 的芯片布局规划过程（左：预训练前；右：预训练后）

芯片平面布局规划方法总结：

分区方法（1960s~1980s）：以分治法为核心，将网表和芯片布局递归划分为足够细颗粒的问题；该方法求解速度快，但会牺牲芯片设计方案的整体质量，可能导致路由堵塞问题
模拟退火法（1980s~2000s）：启发式随机搜索，能生成高质量的芯片设计方案；但算法的收敛速度慢，难以并行化，无法满足 1990s 后日益复杂的电路问题
分层分区（1990s~2000s）：先使用高效的二次规划方法进行初步的布局，再使用启发式的图划分算法进行局部优化，微调节点位置；兼具全局和局部优化的优势
FD (Forced Directed) 算法（1990s~2000s）：基于模拟物理系统动力学来考虑元件之间的拓扑关系和几何约束，寻找系统整体能量最低的稳定状态；该方法的精度高于分层分区，但计算量大
现代分析方法（2010s~2020s）：（1）ePlace，基于电场理论的电路布局优化方法，结合了二次规划和模拟物理的优势（2）RePlAce，通过引入局部密度函数来进一步优化 ePlace（3）DREAMPlace，借助深度学习和 GPU 对 RePlAce 进行加速，但最终精度与 RePlAce 相当
基于学习的方法（2019）：训练一个模型来预测给定宏布局的 DRC 违规数量
端到端学习（本文）：通过梯度更新来优化目标函数，用神经网络近似非线性求解器

注意区别：DREAMPlace 的重点是面向标准单元层次的布局优化，而不是面向宏层次的布局优化；而本文提出AlphaChip 则重点是面向宏层次的布局优化

2.2 模型细节

整体设计与训练概述：

首先定义芯片布局的初始画布（Chip canvas）为 $s_0$，之后基于强化学习的 Agent 考虑宏的放置位置（对应动作 $a_0$），重复以上过程，直到所有的宏均放置完成（对应动作 $a_{T-1}$）
当所有的宏放置完成后，借助 Forced Directed 算法来实现标准单元的放置
需要注意的是，在电路组件放置完成前，每一个动作对应的奖励 $r_0,...,r_{T-1}$ 均为 0
电路组件放置完成后，计算本次迭代后的芯片布局奖励：$r_{T}=-\mathrm{Wirelength}-\lambda\times\mathrm{congestion}-\gamma\times\mathrm{density}$；该奖励是近似线长、拥挤度和组件密度的线性组合，用于指导 Agent 的迭代优化

2.2.1 问题定义

将芯片布局规划问题重新表述为顺序马尔可夫决策过程（MDP），其包含四个要素：

状态空间，对所有布局信息进行编码，包括网表图（邻接矩阵）、节点特征（宽度、高度、类型）、边特征（连接数）、当前需要布局的节点（宏）以及网表图对应的元数据（路由分配、线路总数、宏和标准单元簇）
动作，将宏可以放置在其上的所有可能位置（芯片画布中的网格单元）
状态转移概率，根据当前状态和动作，给出下一步状态的概率分布
奖励，所有中间动作的奖励为 0，只有布局完成的最后一个动作有奖励

核心问题：需要定义一个神经网络，给出累积奖励最大化下的最佳动作

目标函数： $$ J(\theta,G)=\frac{1}{K}\Sigma_{g\sim G}E_{g,p\sim \pi_{\theta}}[R_{g,p}] $$

其中 $g$ 表示一个网表，$G$ 表示 $K$ 个网表的集合
$\pi$ 表示策略网络输出的策略分布，其中的可训练参数为 $\theta$
给定网表 $g$ 和布局 $p$ 的情况下，策略的预期奖励为 $E_{g,p}[R_{g,p}]$

$$E_{g,p}[R_{g,p}]=\mathrm{Wirelength}(g,p)-\lambda \mathrm{Congestion}(g,p)-\gamma \mathrm{Density}(g,p)$$

在本文实验中，设置超参数 $\lambda=0.01$，$\gamma=0.01$；密度最大值为 0.6（硬约束）

2.2.2 策略和价值网络

策略和价值网络的整体架构：

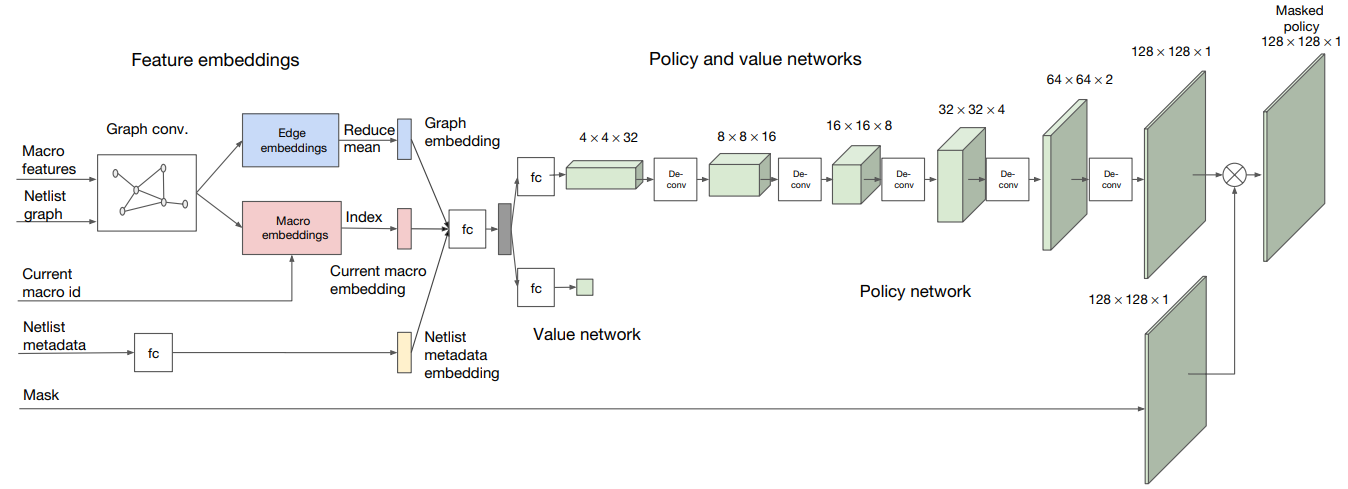
策略和价值网络的输入包括宏特征、网表图、当前宏、网表的元数据和密度掩码（Mask）
价值网络（Value network）输出预测奖励，而策略网络（Policy network）输出预测动作
价值网络使用包含 1w 条数据集进行训练，数据包含芯片设计布局及其相应的奖励标签
训练后的价值网络作为策略网络的编码器层，对网表相关的数据进行嵌入表示（比如宏信息转化为节点嵌入、网表图转化为图嵌入等），提炼成可用于下游任务的低维向量表示
上图中，Graph conv 表示图卷积神经网络，fc 表示全连接层，De-conv 表示反卷积层

Edge-GCN 图卷积神经网络：

Edge-GCN 主要用于策略和价值网络中节点嵌入和图嵌入的生成
定义节点 $i$ 的节点嵌入为 $v_i$ ，节点 $j$ 的节点嵌入为 $v_j$，则两节点之间边的嵌入可表示为 $e_{ij}$。在 Edge-GCN 中，边嵌入 $e_{ij}$ 的迭代更新公式如下（$w_{ij}^{\mathrm{e}}$ 为可学习的参数）：

$$ e_{ij}=\mathrm{fc}_{e}(\mathrm{concat}(v_{i}|v_{j}|w_{ij}^{\mathrm{e}})) $$

节点嵌入则根据邻接边嵌入的聚合信息进行更新：

$$v_{i}=\mathrm{mean}_{j\in\mathrm{Neighbours}(v_{i})}(e_{ij})$$

在训练阶段，Edge-GCN 借助有监督数据（X 为宏特征和网表图，y 为奖励）进行梯度计算和参数更新，最终 Edge-GCN 将实现节点信息和边信息的有效嵌入表示

2.2.3 策略网络的训练

策略网络的核心要素：

状态 $s_t$，时刻 $t$ 的状态嵌入包含图嵌入，节点嵌入，元数据嵌入
动作空间，当前节点放置在网格中每个单元上的可行性（密度掩码）
动作 $a_t$，策略网络在时刻 $t$ 对当前节点的放置位置推测
奖励 $r$，直接来自价值网络的预测输出（所有中间动作的奖励为 0）
网络参数 $\theta$，以最大化累积奖励为目标，用 PPO 算法更新策略网络

优化目标-最大化累积奖励函数：

奖励是近似线长、拥挤度和组件密度的加权和
软约束：较低的拥挤度会改善奖励函数
硬约束：屏蔽组件密度大于特定阈值的情况

为了保证每次迭代的运行时间足够小，需要简化奖励函数的计算

奖励函数的简化：

聚类算法加速标准单元的布置。用 hMETIS（一种基于最小切割目标的图分区技术）将数百万个标准单元划分为几千个簇，再用 FD 方法放置标准单元簇，实现近似而快速的标准单元布局
将布置的网格进行离散化处理。所有宏或标准单元簇的放置中心位于网格单元的中心
使用半周长线长（HPWL）对线长近似。HPWL 定义为网表中所有节点的边界框的半周长（其中 $x_b$ 和 $y_b$ 表示网络 $i$ 中的一个端点坐标，$q_i$ 是归一化因子）： $$

\mathrm{HPWL}(i)=(\max_{b=i}{x_{b}}-\min_{b=i}{x_{b}}+1)

+(\max_{b=i}{y_{b}}-\min_{b=i}{y_{b}}+1) $$ $$ \mathrm{HPWL}(\mathrm{netlist})=\sum_{i=1}^{N_{\mathrm{netlist}}}q(i)\mathrm{HPWL}(i). $$

简化拥挤度的计算。先用卷积核分别从水平方向和垂直方向抽样统计每个网络单元的空余布置资源，再使用排名前 10%的拥挤度均值，作为最终布局方案的拥挤度近似估计

用于策略网络的参数更新的 PPO 方法，其目标函数如下： $${\cal L}^{\mathrm{CLIP}}(\theta)=\hat{E}_{t}[\operatorname*{min}(r_{t}(\theta)\hat{A}_{t},\operatorname*{clip}(r_{t}(\theta), 1-\varepsilon, 1+\varepsilon)\hat{A}_{t})]$$

其中 $\hat{E}_{t}$ 表示时刻 $t$ 时的期望值
$r_t$ 是时刻 $t$ 时新策略与旧策略的预测动作概率比：$r_t(\theta)=\frac{\pi \theta_{new}(a_t/s_t)}{\pi \theta_{old}(a_t/s_t)}$
$\hat{A}_{t}$ 是时刻 $t$ 时新策略的预测动作，相比于旧策略的奖励增加值，即估计优势

2.3 其他算法细节补充

基于物理模拟的 FD 算法（简单描述）：

将网表转化为一个弹簧系统，根据节点的权重和距离对每个节点施加力
紧密连接的节点间会相互吸引，而重叠的节单间会相互排除（降低组件密度）
弹簧系统构造完成后，根据节点的施力情况移动节点（沿着合力的方向）
为了减少震荡，约束每次移动的最大距离

模拟退火 SA 算法（简单描述）：

在每次迭代中，执行 2N 次宏操作（N 表示宏的数量）
宏操作类型包括三种，每种操作的执行概率为 1/3：（1）随机交换两个宏的位置（2）随机移动一个宏到邻近的空白位置（3）镜像，对选择的宏沿着 x 轴或 y 轴进行随机翻转
当完成宏操作后，再使用 FD 算法来放置标准单位簇，同时固定宏的位置
对于每一个宏操作或 FD 操作，当新状态能降低成本/增加奖励时则会被接受，否则以 $p=exp(\Delta_{cost}/t)$ 的概率被接受；其中 $t$ 为温度参数，随着迭代次数的增加逐渐降低（冷却）

2.4 实验分析

不同策略的性能对比：

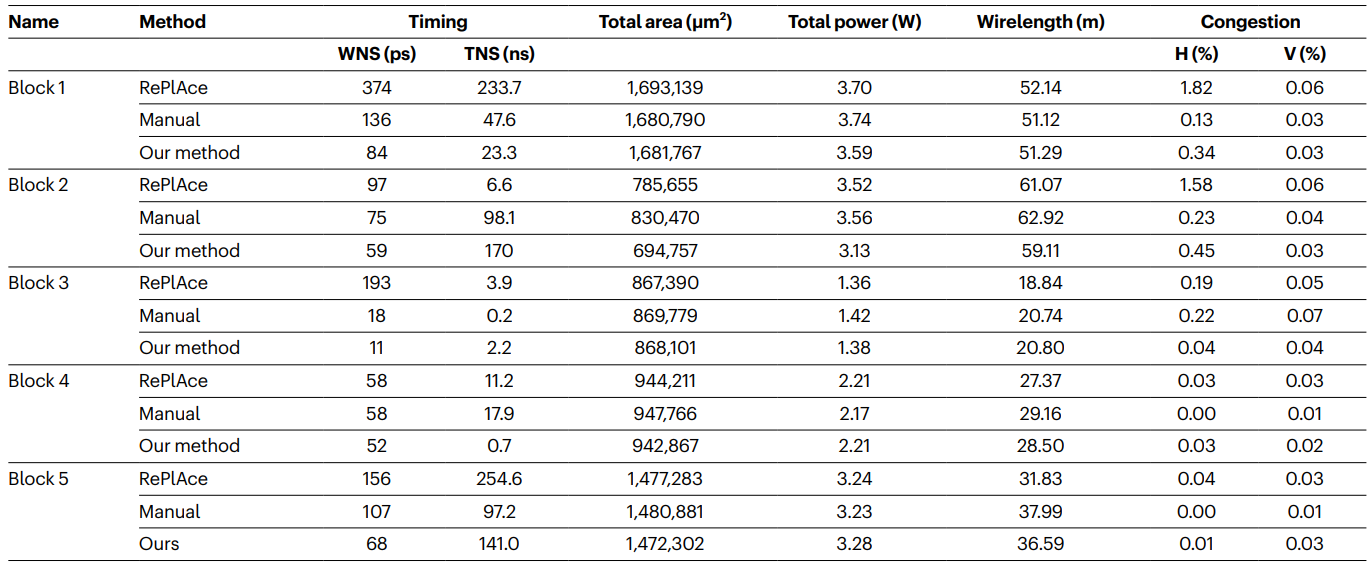
上图列举了不同算法在 5 种芯片模块上的性能指标对比
性能指标包括延迟（总裕度 TNS 和最差负裕度 WNS，负裕度描述了信号延迟超过预期延迟程度）、面积、功耗、线长和拥挤度（水平 H 和垂直 V），所以性能指标都是越小越好
RePIAce 是当前的 SOTA 方法；Manual 指人类专家使用 EDA 工具完成设计

策略网络的预训练和微调：

预训练过的策略网络微调效果明显优于从头开始训练的策略网络

不同数据集下的预训练和微调：

随着数据集的增加，算法收敛速度和最终布局质量均有明显改善

Zero-shot 性能对比，Edge-GCN vs GCN：

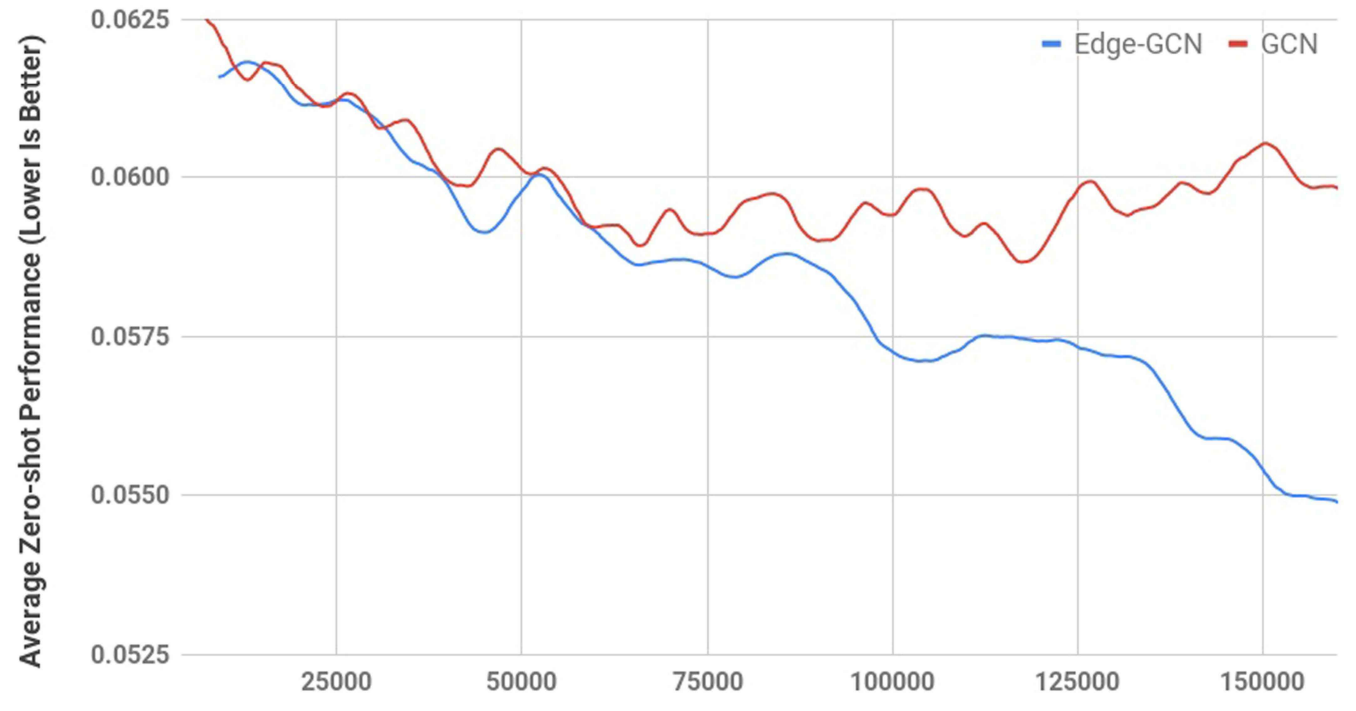
Edge-GCN 具备更强的模型泛化能力，能适应更多未见过的芯片布局

放置策略可视化（zero-shot VS 微调）：

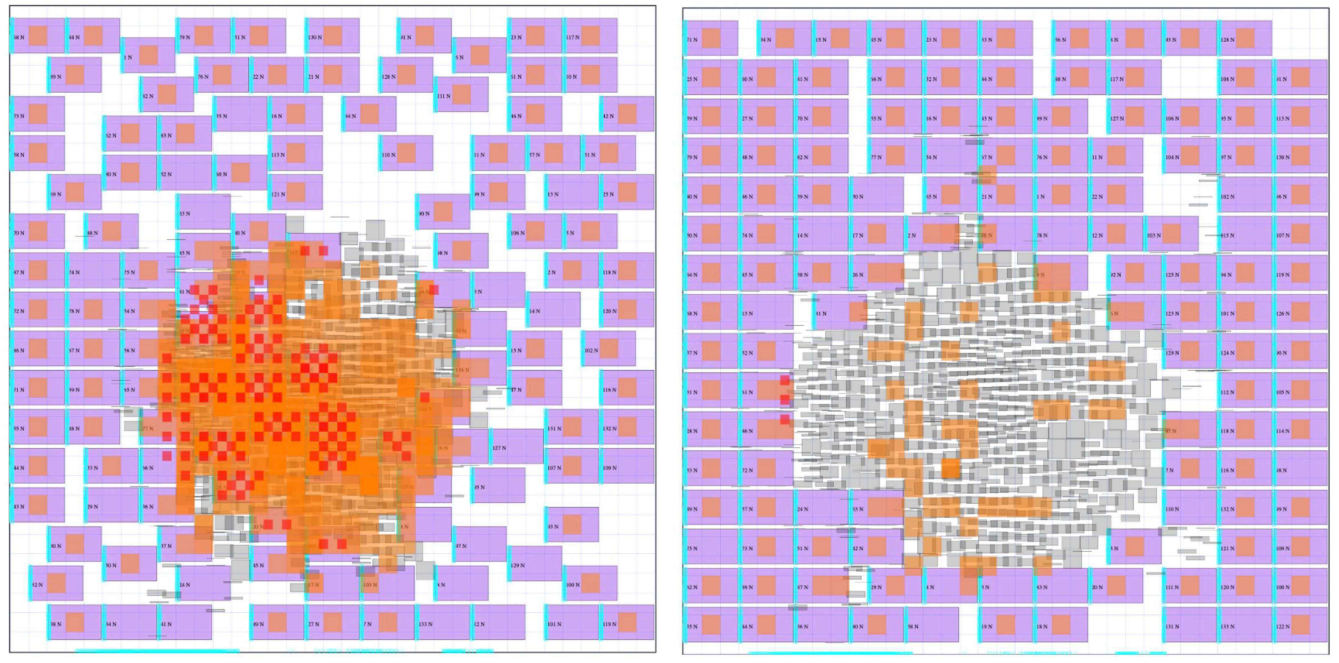
Zero-shot 的情况下，策略网络也会在网格中心预留标准单元的放置空间；这种行为能减少线长，说明了预训练的策略网络具备较好的迁移能力；当然微调后的布局质量会更高

消融实验，寻找最佳的拥挤度权重：

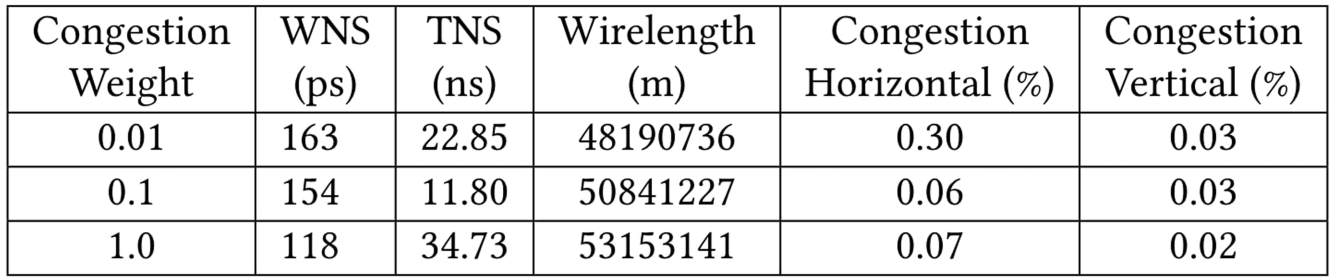
拥挤度的权重增加，明显改善了布局延迟、垂直和水平方向的拥挤度
但与之相对应的，布局的线长也会明显增加；因此二者之间需要权衡
用 0.1 作为拥挤度权重，能在保持较低延迟和拥挤度的同时避免线长过大

抗噪声实验：选择不同的随机种子对最终布局的性能影响可忽略（偏差约 0.22%）

后记

论文附录中还有一张自研的 GPU 芯片的真实图片，但是被打码了，啥也看不着...

2022 年 4 月，AlphaChip 解决了之前开源代码的可用性问题

2023 年 9 月，AlphaChip 一文因细节缺乏与可复现性有限受到质疑

2024 年 11 月，开源了预训练的模型文件（官方不推荐直接用）

2024 年 11 月，谷歌 Deepmind 团队的官方博客文章补充：

AlphaChip 已用于另外三代谷歌旗舰 AI 加速器张量处理单元 (TPU)
随着每一代 TPU 的不断发展，AlphaChip 与人类专家之间的性能差距不断扩大。与人类专家相比，TPU v5e 线长减少了 3.2% ；TPU v5p 线长减少了 4.5%；Trillium 30 中线长减少了 6.2%
芯片制造商联发科通过 AlphaChip 加速其最先进芯片的开发，改善功耗、性能和面积

Deepmind 团队的 Alpha 系列模型对比：

模型类型	年份	领域	状态空间	基础架构	更新策略	算法辅助	约束
AlphaGo Zero	2017-10	围棋	~10^360	CNN	自我对弈	MCTS	围棋规则
AlphaChip	2021-06	芯片设计	>10^2500	Edge-GCN	PPO	FD 物理模拟	线长和密度
AlphaFold2	2021-08	蛋白质	历史库	Evoformer	端到端	OpenMM	刚性，结构
AlphaGeometry	2024-01	数学几何	定理合成	LLMs	微调	推理引擎	规则，辅线

都具备丰富多模态化的数据输入，由此而设计的网络基础结构也各有不同；
都可以用游戏化的思维，量化策略、奖励和状态；也都有游戏规则的约束
站在巨人的肩膀上，大部分依托于已有的数据累积、推理引擎、算法模拟
基础架构逐渐迭代升级，从最初的CNN、GCN，再到后来的 Transformer 和 LLMs

个人笔记

Digital Garden | 王半仙