1 基础时序方法
均值回归：对历史一段时间的值取平均，作为未来每个时刻的预测
指数平滑：预测值是过去一段时间内观测值（或已预测值）的加权平均值
普通回归预测：借助时序相关特征（如节假日、周期性）实现建模预测
更多时序类衍生特征可参考 tsfresh概述
2 ARIMA
自回归（AR）模型：
- 用变量自身的历史时间数据对变量进行预测
- AR 模型需要满足时序平稳性的要求，时序间需要存在自相关性
- p 阶 AR模型的公式定义如下：$y_t=\mu+\Sigma_{i=1}^p\gamma_iy_{t-i}+\epsilon_t$
- 其中 $\mu$ 表示常数项，$\gamma$ 表示自相关系数，$\epsilon$ 表示残差
移动平均（MA）模型：
- MA 模型关注的是自回归模型中的误差项累加
- q 阶 MA 模型的公式定义如下：$y_t=\mu+\epsilon_t+\Sigma_{i=1}^p\theta_i \epsilon_{t-i}$
- MA 模型能有效消除预测中的随机波动
自回归移动平均（ARMA）模型：
- ARMA (p, q) 模型是p 阶 AR 模型和 q 阶 MA 模型的组合
- ARMA (p, q) 的公式如下：$y_t=\mu+\Sigma_{i=1}^p\gamma_iy_{t-i}+\epsilon_t+\Sigma_{i=1}^p\theta_i \epsilon_{t-i}$
- ARMA 假设时序可以由其自身的过去或滞后值以及随机扰动项来解释
AR、MA、ARMA 模型的选择:
- 若偏自相关函数是截尾的，而自相关函数是拖尾的，则建立 AR 模型；
- 若偏自相关函数是拖尾的，而自相关函数是截尾的，则建立 MA 模型；
- 若偏自相关函数和自相关函数均是拖尾的，则序列适合 ARMA 模型
ARMA 模型的定阶：
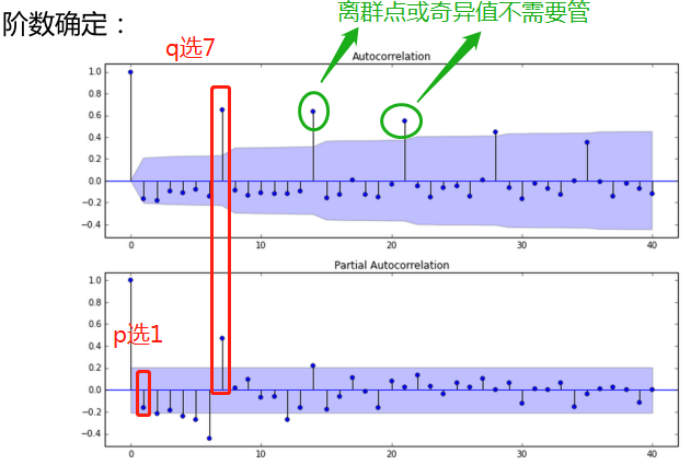
| 模型 | 自相关 ACF | 偏自相关 PACF |
|---|---|---|
| AR (p) | 衰减趋于 0 | P 阶后截尾 |
| MA (q) | q 阶后截尾 | 衰减趋于 0 |
| ARMA (p, q)) | q 阶后衰减趋于 0 | P 阶后衰减趋于 0 |
ARIMA ：考虑 d 阶差分的 ARMA
- 平稳性要求序列的均值和方差不发生明显变化
- 对于平稳/弱平稳时序，可以直接使用 ARMA 模型实现建模预测
- 对于非平稳时序，需要先通过差分的方式实现序列的平稳（有时候需要重复多次差分才能实现序列的平稳），再根据 ACF 和 PACF 图确定阶数，最后使用 ARMA 进行建模。
3 其他
Prophet：Facebook 开源的时序预测算法 17.5 k ⭐
- 基于加法模型进行时序预测，综合考虑非线性趋势、周期性和节假日影响
- 对于缺失数据和趋势变化具有鲁棒性，并且通常能够很好地处理异常值
AutoTS：时间序列包，旨在大规模快速部署高精度预测 955⭐
- 支持 sklearn 内嵌的数十种可用模型，包括统计方法、机器学习、深度学习
- 支持多时序预测输出和概率（上下限）预测；支持用户自定义外生回归变量
- AutoML 特征搜索，寻找最佳的模型、预处理和集成方法；评估指标丰富
神经网络系列：