个人笔记

• 原始标题：KAN: Kolmogorov-Arnold Networks
• 发布平台：预印本
• 发布日期：2024-05-24
• 引用量（非实时）：15
  • 1 文章萃取
    • 1.1 核心观点
    • 1.2 综合评价
    • 1.3 主观评分：⭐⭐⭐⭐⭐
  • 2 精读笔记
    • 2.1 背景知识
    • 2.2 KAN 网络原理
    • 2.3 MLP vs KAN
    • 2.4 KAN 能力评估
    • 2.5 KAN 的实验分析
• 后记
• 相关资源

原始标题：KAN: Kolmogorov-Arnold Networks

发布平台：预印本

发布日期：2024-05-24

引用量（非实时）：15

DOI：

作者：Ziming Liu, Yixuan Wang, Sachin Vaidya, Fabian Ruehle, James Halverson, Marin Soljačić, Thomas Y. Hou, Max Tegmark

关键字： #KAN #MLP

文章类型：preprint

品读时间：2024-06-06 10:35

1 文章萃取

1.1 核心观点

本文受柯尔莫哥洛夫-阿诺德（Kolmogorov-Arnold ）表示定理启发，提出了 KAN 作为 MLP 的有效替代。 KAN 将可学习的激活函数放在边（“权重”）上，每个权重参数都被样条曲线参数化为可学习的一维函数，而 KAN 的节点只是对输入信号进行求和。KAN 还可以通过稀疏正则项进行神经网络的剪枝，以实现更强的可解释性和更直观的可视化。

实验分析表明，KAN 在准确性和可解释性方面优于 MLP，KAN 适合用于发现数学和物理定律；KAN 在训练效率上比 MLP 慢 10 倍，但同等精度下 KAN 网络一般比 MLP 小得多；KAN 存在继续优化计算效率的空间，并为目前的深度学习领域注入了新的活力

1.2 综合评价

• 具备出色的准确率和可解释性，但是计算效率偏低
• 适用于数学物理领域，但在深度网络中的使用前景尚不明确
• 具备较大的潜力和优化空间（更换 B 样条函数、自适应网格）

1.3 主观评分：⭐⭐⭐⭐⭐

2 精读笔记

2.1 背景知识

前置知识：样条函数

定义 0 阶 B 样条（分段常数多项式）如下： $$ \left.B_{i,0}(t):= \left\{\begin{array}{ll}1&\mathrm{if} t_i\leq t<t_{i+1} \\0&\mathrm{otherwise}.\end{array}\right.\right. $$ p 阶 B 样条函数开源通过 Cox-de Boor 递归公式得到： $$ B_{i,p}(t):=\frac{t-t_i}{t_{i+p}-t_i}B_{i,p-1}(t)+\frac{t_{i+p+1}-t}{t_{i+p+1}-t_{i+1}}B_{i+1,p-1}(t) $$

以上公式递归计算的成本较高，实际应用时存在效率问题

后来出的Efficent KAN尝试避免递归计算，实现了 KAN 的加速

通用近似定理（universal approximation theorem）：

• 也称万能近似定理，是多层感知器（MLP）和深度学习的理论依据
• 神经网络可以用来近似任意的复杂函数，并且可以达到任意近似精准度

MLP 的局限性：消耗参数量大；可解释性差（相对于注意力层）

Kolmogorov-Arnold 表示定理：如果 $f$ 是有界域上的多元连续函数，则 $f$ 可以写成单变量连续函数和二元连续函数的有限组合加法运算。更具体地说，对于平滑的 $f:[0,1]^n\to\mathbb{R}$， $$ f(\mathbf{x})=f(x_1,\cdots,x_n)=\sum_{q=1}^{2n+1}\Phi_q\biggl(\sum_{p=1}^n\phi_{q,p}(x_p)\biggr) $$

• 向量 $x$ 的长度为 $n$；其中第 $p$ 个分量 $x_p$ 由一元函数 $\phi_{q,p}$ （单变量连续函数）处理
• $\Phi_q$ 是外部函数（也是一元函数），用于处理 $p$ 个一元函数 $\phi_{q,p}$ 的输出组成的求和
• 任意的连续函数 $f$ 可以表示为有限个单变量函数（$\phi_{q,p}, \Phi_q$）的嵌套组合

KA 定理，描述了任意多变量连续函数可以表示为一系列单变量函数的组合

KA 定理的局限性：一元函数可能是非平滑甚至分形（fractal），导致不可学习

2.2 KAN 网络原理

KAN 通过 B 样条函数来参数化 $\phi_{q,p}, \Phi_q$ 这些单变量函数，并通过组合这些函数来构建整个网络。以一个二层 KAN 网络为例，其结果如下图所示：

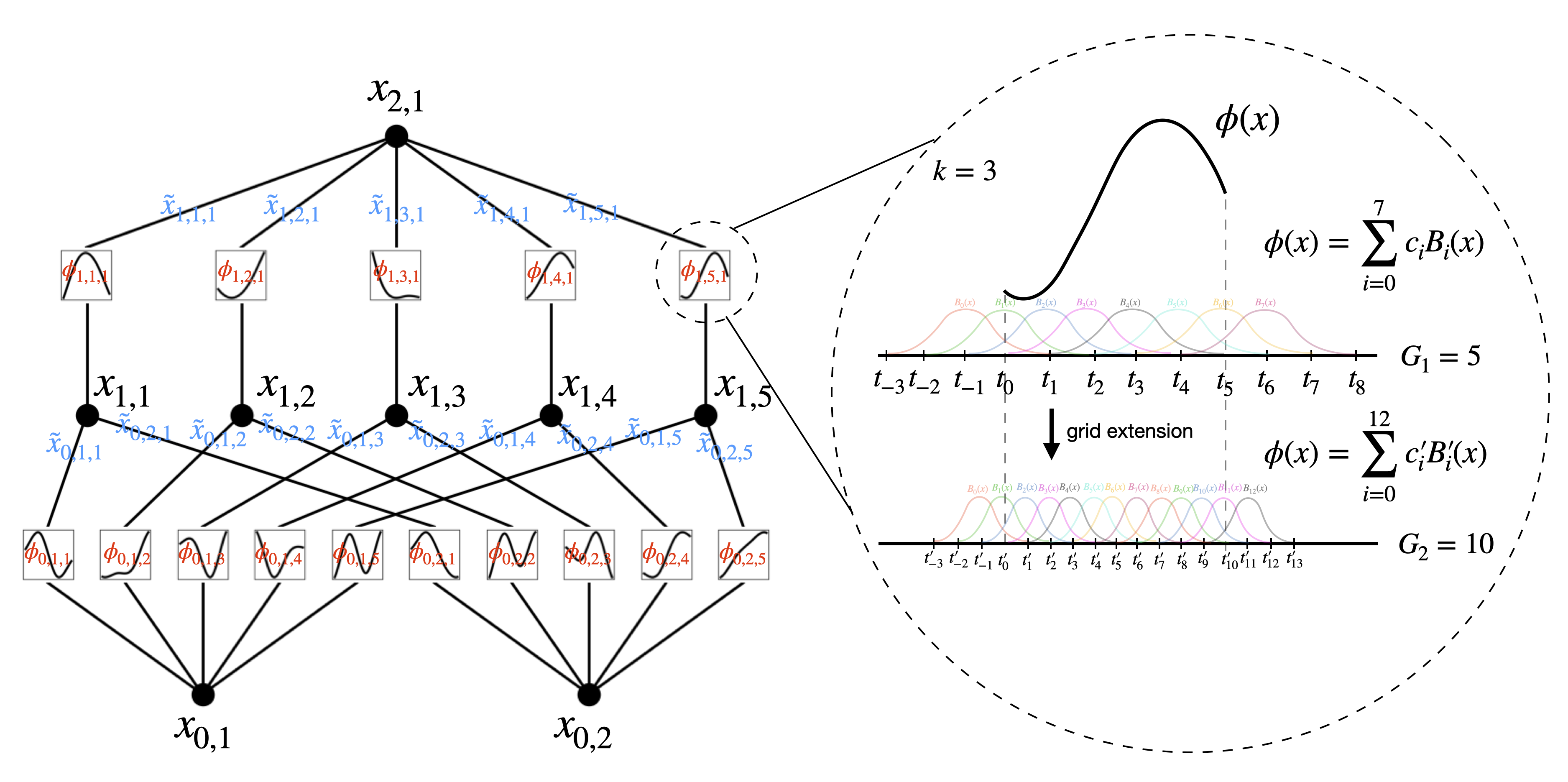
• 具有 $n_{in}$ 维输入和 $n_{out}$ 维输出的 KAN 层可以定义为一维函数矩阵 $\Phi={\phi_{q,p}}$，其中函数 $\phi_{q,p}$ 具有可训练参数。当 $n_{in}=n,n_{out}=2n+1$ 时，两个 KAN 层即可表示 KA 定理的公式形式
• 每个一维函数则是 B 样条函数的参数化表示，即多个基函数 $B(x)$ 的线性组合；其中 $k=3$ 描述了 B 样条的阶数，$G$ 描述了间隔数/分段 B 样条数（$G$ 越大网格越细密）
• $l+1$ 层的第 $j$ 个神经元的预激活值 $x_{l+1,j}$ 来自前一层的后激活值的总和 $\sum_{i=1}^{n_{l}}\widetilde{x}_{l,j,i}$： $$

x_{l+1,j}=\sum_{i=1}^{n_{l}}\widetilde{x}_{l,j,i}=\sum_{i=1}^{n_{l}}\phi_{l,j,i}(x_{l,i}),\quad j=1,\cdots,n_{l+1}. $$

• 给定输入向量 $x_o$，假设第 $i$ 层的输出维度为 $n_i$，由 $L$ 层组成的 KAN 网络可表示如下：

$$ f(\mathbf{x})=\sum_{i_{L-1}=1}^{n_{L-1}}\phi_{L-1,i_{L},i_{L-1}}\biggl(\sum_{i_{L-2}=1}^{n_{L-2}}\cdots\biggl(\sum_{i_{2}=1}^{n_{2}}\phi_{2,i_{3},i_{2}}\biggl(\sum_{i_{1}=1}^{n_{1}}\phi_{1,i_{2},i_{1}}\biggl(\sum_{i_{0}=1}^{n_{0}}\phi_{0,i_{1},i_{0}}(x_{i_{0}})\biggr)\biggr)\biggr)\cdots\biggr) $$

• 为了表示形式显得更清晰直观，可简化 $L$ 层的 KAN 网络的形式如下：

$$ f(\mathbf{x})=\mathrm{KAN}(\mathbf{x})=(\mathbf{\Phi}_{L-1}\circ\mathbf{\Phi}_{L-2}\circ\cdots\circ\mathbf{\Phi}_{1}\circ\mathbf{\Phi}_{0})\mathbf{x} $$

网格扩展（grid extension）在 2.4 节有更详细的描述

KAN 网络的细节优化：

1. 调整残差激活函数：$\phi(x)=w_bb(x)+w_sspline(x)$
   • 其中 $b(x)=x/(1+e^{-x})$ 是基函数（basis function），类似残差连接
   • $spline(x)$ 被参数化为 B 样条的线性组合：$spline(x)=\Sigma_ic_iB_i(x)$
   • 权重参数 $w_b$ 和 $w_s$ 默认是可训练的；原则上这两个参数是冗余的（可吸收到 $b(x)$ 和 $spine(x)$）中，此处权重参数设计在函数外面，是为了更好地控制激活函数的整体大小
2. 约束初始化的尺度：$w_s=1, spline(x)\approx 0$ \
   • 权重参数 $w_s$ 使用 Xavier 初始化（服从均匀分布 $U\Big[-\frac{\sqrt{6}}{\sqrt{n_j+n_{j+1}}},\frac{\sqrt{6}}{\sqrt{n_j+n_{j+1}}}\Big]$）
   • B 样条的系数 $c_i$ 初始化满足 $N (0, \sigma^2)$，其中 $\sigma=0.1$
3. 样条网格（spline grids）的更新：根据输入激活值动态更新每个网格，避免在训练时激活值超出固定区域（splines 定义的有界区域）的问题。
   • 其他方法：（a）通过梯度下降学习网格（b）使用归一化使输入范围固定

2.3 MLP vs KAN

为方便对比，将 $L$ 层的 MLP 网络的形式展示如下： $$ \mathrm{MLP}(\mathbf{x})=(\mathbf{W}_{L-1}\circ\sigma\circ\mathbf{W}_{L-2}\circ\sigma\circ\cdots\circ\mathbf{W}_{1}\circ\sigma\circ\mathbf{W}_{0})\mathbf{x} $$

KAN 网络将线性变换 $\mathbf{W}$ 和非线性激活 $\sigma$ 一起视为 $\mathbf{\Phi}$

MLP vs KAN：

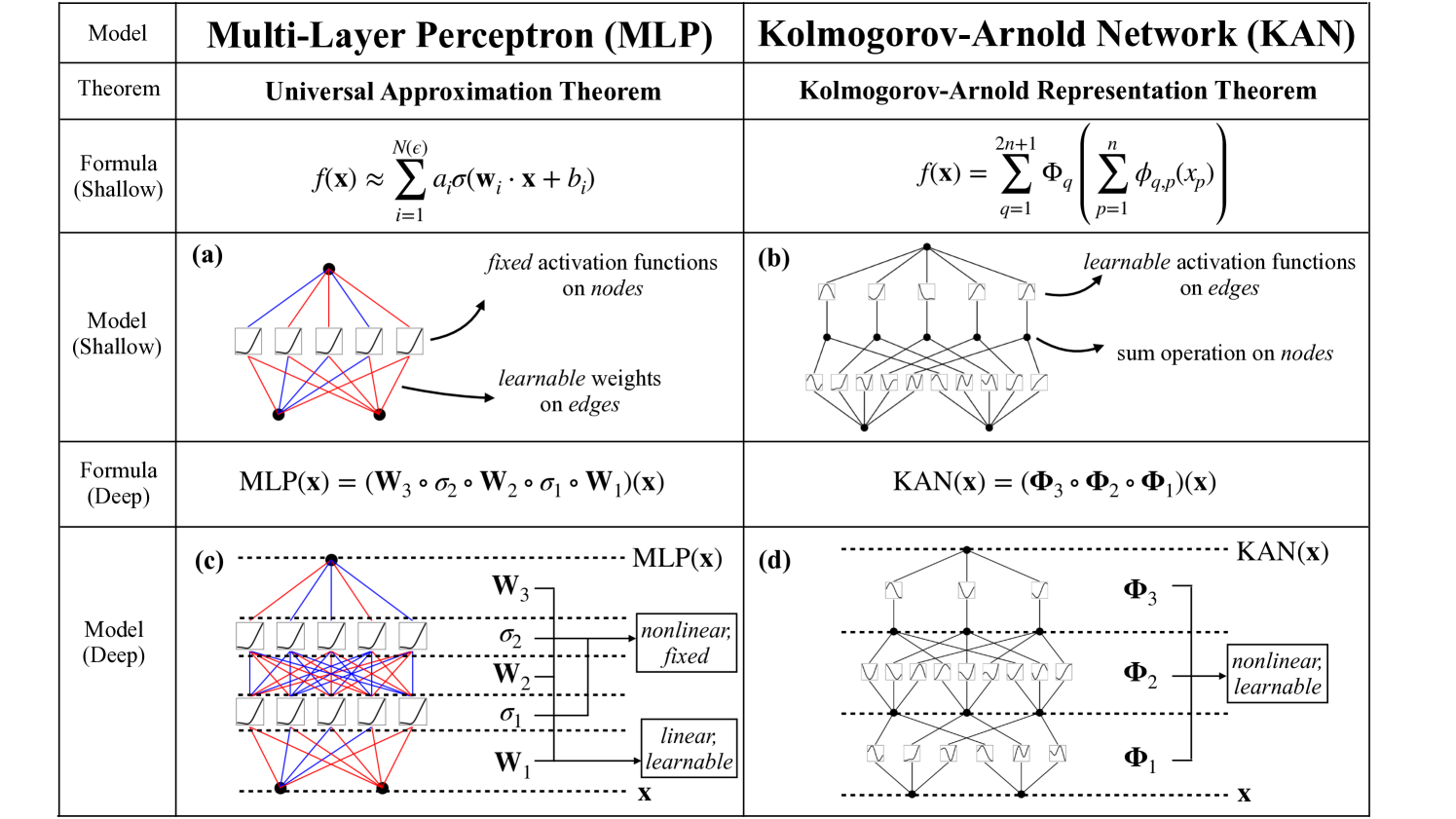
• （a）MLP 在节点上进行非线性激活，在训练过程中调整边参数
• （b）KAN 在边上进行非线性激活和训练，在节点上进行求和操作
• （c）MLP 将线性变换 $\mathbf{W}$ 和非线性激活 $\sigma$ 分开处理，交替执行
• （d）KAN 将全部的一维函数操作 $\phi$ 合并在 $\mathbf{\Phi}$ 中（包含线性/非线性）

KAN 使用可学习的一维函数取代权重参数，并将一维函数参数化为样条函数

KANs 是 splines 和 MLP 的组合，结合了各自的优势：

• Splines 在低维函数中是准确的，易于局部调整，能够在不同分辨率之间切换；但是当 N 过大时，Splines 会因为 COD（维度灾难， curse of dimensionality）问题而失败
• MLP 可以自动学习特征及其组合，也没有那么严重的 COD 问题；但在低维度下比 Splines 不够准确，面对某些高维函数，使用 ReLU 激活函数来近似指数和正弦函数非常低效
• KANs可以很好地学习组合结构和单变量函数，因此在性能上远远优于MLPs

在 KANs 和 MLPs 之间该如何抉择：

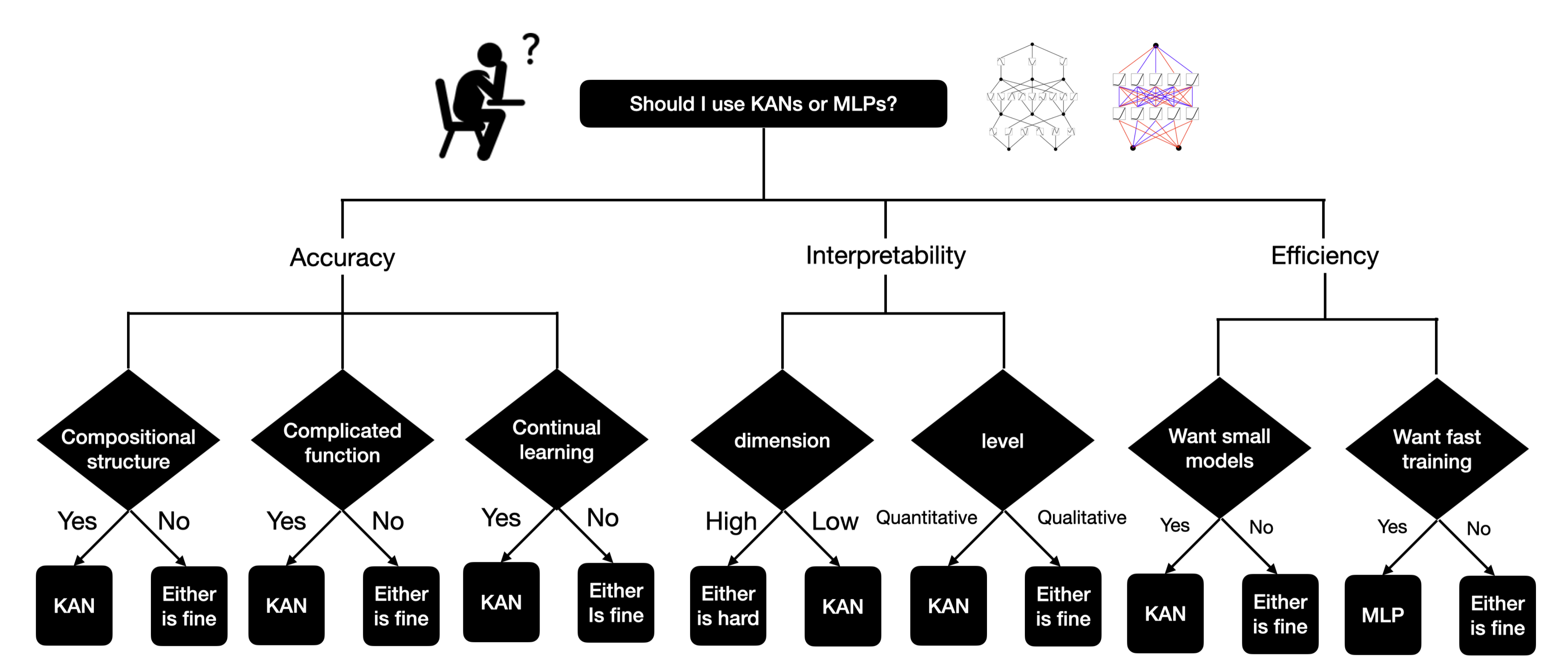
• KANs 最大的瓶颈在于其训练速度较慢。相同参数量下，KANs 通常比 MLPs 慢10倍
• 在其他情况下，KANs 应该与 MLPs 相当或更好（无论是可解释性，还是准确率）

KANs 的训练速度较慢是一个需要持续改进的工程问题，而不是一个基本限制

2.4 KAN 能力评估

1. KAN 的拟合能力

   对于任意的 $0\leq m \leq k$ ，KAN 网络拟合的误差近似界限为： $$

||\left(\Phi_{L-1}^G\circ\Phi_{L-2}^G\circ\cdots\circ\Phi_1^G\circ\Phi_0^G\right)\mathbf{x}||_{C^m}\leq CG^{-k-1+m} $$

• 等式左侧表示 $C^m$ 范数（函数空间具有连续导数直到 $m$ 阶的）下的拟合误差，一个较小的 $C^m$ 范数误差意味着近似解在整个定义域上及其导数上与真实解非常接近
• 常数 $C$ 取决于 $f$ 及其表示形式；$G$ 描述了网格尺寸（$G$ 越大网格越细密）
• $-k-1+m$ 描述了 B 样条的拟合能力；$k$ 表示 B 样条的阶数（一般为 3）
• 选择合适的网格尺寸 $G$ 和 spline 阶数 $k$，KAN 能够达到所需的近似精度

以地图绘制为例来理解，网格越密集（$G$ 越大）则绘制的地图分辨率越高，每个网格内的细节越丰富（$k$ 越大），最终绘制的地图越接近真实的地形

关于该误差近似界限的证明可参阅原始论文 2.4 节

2. KAN 的网格扩展

KAN 可以先保持较粗的网格（$G_1=5$）以降低参数量并进行训练，然后再细化网格（$G_2=10$）以扩展为具有更多参数的 KAN，而无需重新开始训练较大的模型。不过粗网格中的基函数组合 $c_iB_i(x)$ 需要重新调整权重得到新的基函数组合 $c'_iB'_i(x)$： $$ {c_j^{'}}=\underset{{c_j^{'}}}{\operatorname*{argmin}}\underset{\mathrm{x\sim p(x)}}{\operatorname*{\mathbb{E}}}\Bigg(\sum_{\mathrm{j=0}}^{\mathrm{G_2+k-1}}\mathrm{c_j^{'}B_j^{'}(x)}-\sum_{\mathrm{i=0}}^{\mathrm{G_1+k-1}}\mathrm{c_i}\mathrm{B_i(x)}\Bigg)^2 $$

• 以上公式通过 最小二乘法 寻找最优的权重（追求调整前后的 $\phi$ 不变）

KAN 网格扩展的实验分析：

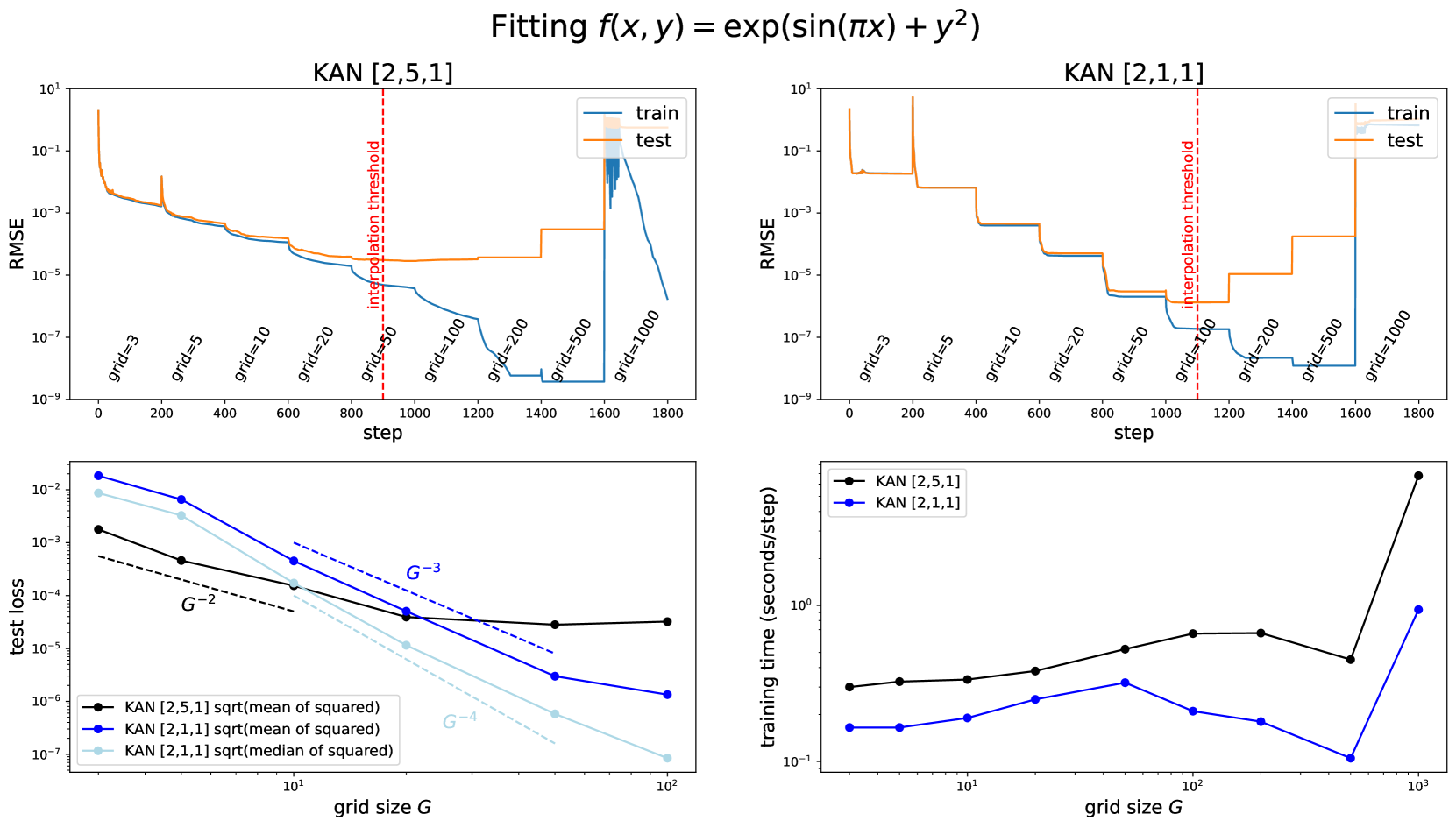
• 伴随着迭代次数的增加，RMSE 随着网格密度的调整实现阶梯式下降；相比于参数量较大的 KAN（左上），较低参数量的 KAN（右上）阶梯更明显，最优 RMSE 对应的 G 阈值也更高
• 伴随着网格尺寸 G 的增加，KAN 的测试集损失呈下降趋势而训练时间在逐步增长

由于实验中的 KAN 总参数量约为 15G，因此本文期望的 G 阈值为样本数/15（实验符合预期）

3. KAN 的可解释性

KAN 通过添加稀疏正则项来进行剪枝，提高了 KAN 的可解释性。最终的训练目标 $\ell_{\mathrm{total}}$ 包含预测损失 $\ell_{\mathrm{pred}}$，所有激活函数的L1 正则项，所有 KAN 层的熵正则项三个部分：

$$\ell_{\mathrm{total}}=\ell_{\mathrm{pred}}+\lambda\Bigg (\mu_{1}\sum_{l=0}^{L-1}\left|\Phi_{l}\right|_{1}+\mu_{2}\sum_{l=0}^{L-1}S (\Phi_{l})\Bigg) $$

• 所有激活函数 $\phi$ 的 L1 正则：$\left|\Phi\right|_{1}\equiv\sum_{i=1}^{n_{\mathrm{in}}}\sum_{j=1}^{n_{\mathrm{out}}}\left|\phi_{i,j}\right|_{1}$
• 所有 KAN 层的熵正则项：$S(\Phi)\equiv-\sum_{i=1}^{n_{\mathrm{in}}}\sum_{j=1}^{n_{\mathrm{out}}}\frac{\left|\phi_{i,j}\right|_{1}}{\left|\Phi\right|_{1}}\mathrm{log}\Bigg(\frac{\left|\phi_{i,j}\right|_{1}}{\left|\Phi\right|_{1}}\Bigg)$
• 其中 $\mu_1,\mu_2$ 是相对幅度，通常设置为 1 ， $\lambda$ 控制整体正则化幅度

KAN 进行符号回归的示例：

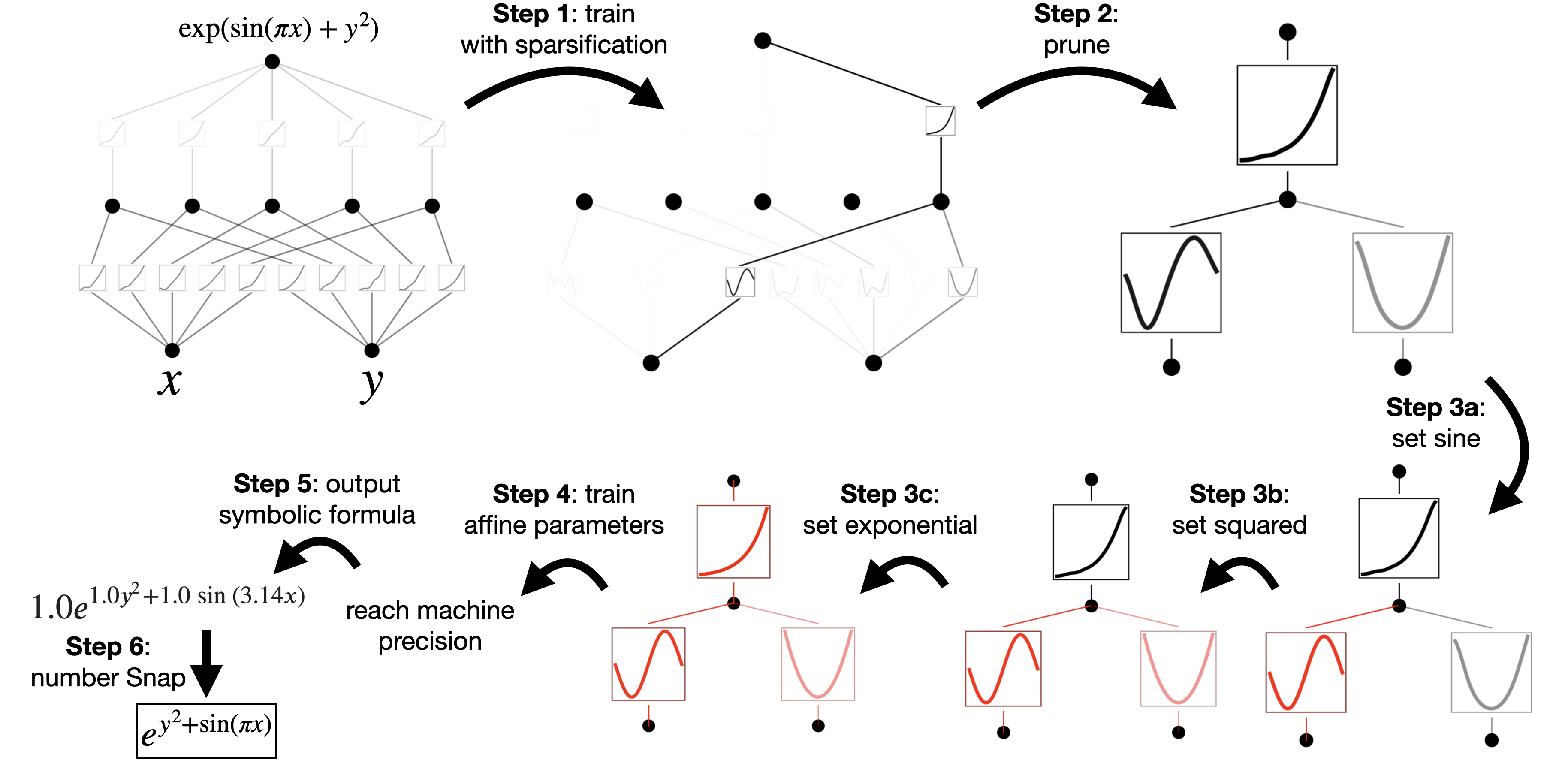
2.5 KAN 的实验分析

在各种任务中，KAN 接近最优的缩放定律（随着参数量的增加而损失快速降低）

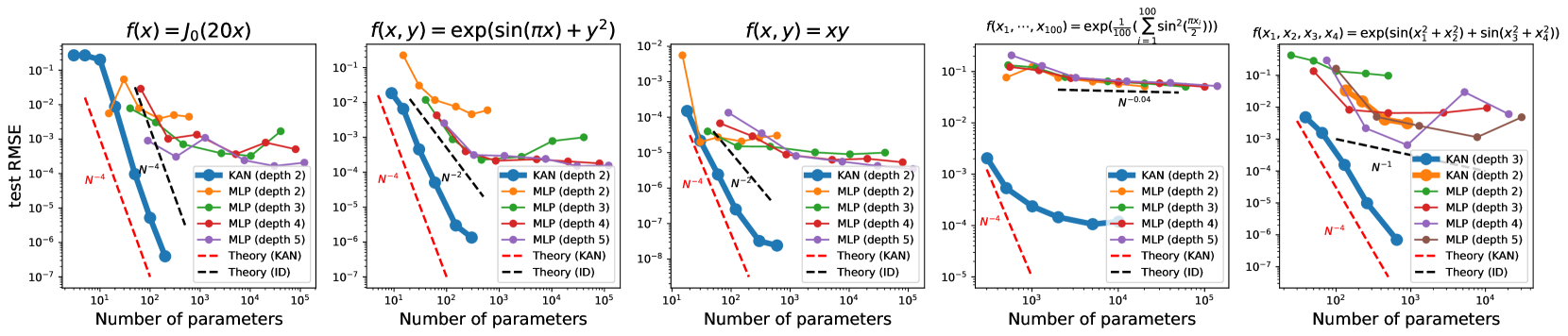
在所有特殊函数的拟合中，KAN 比 MLP 具有更好的帕累托前沿（性能在多目标中始终最优）

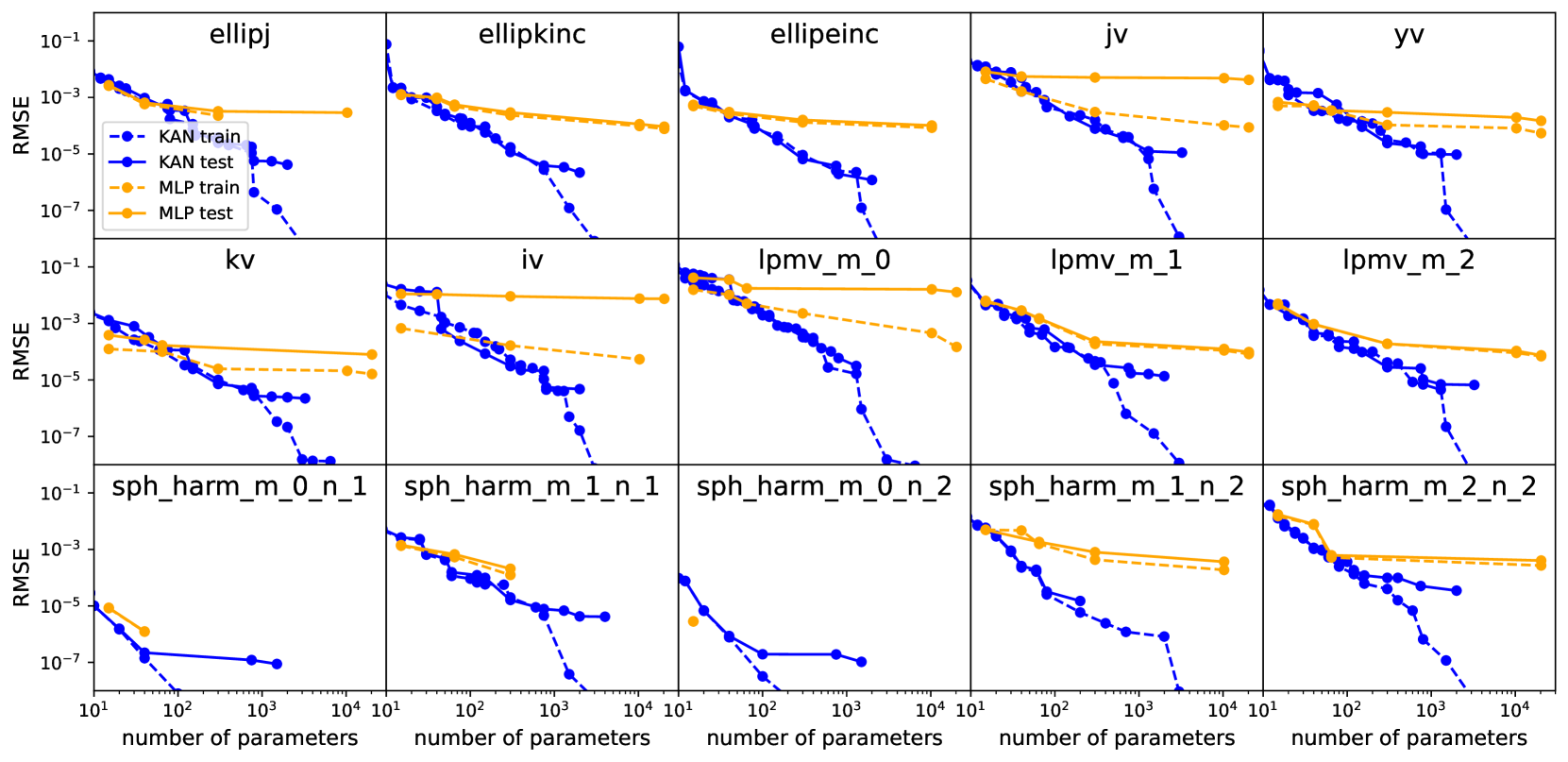
• KAN 可以自然地在持续学习中发挥作用，而不会出现灾难性遗忘（边学边忘）

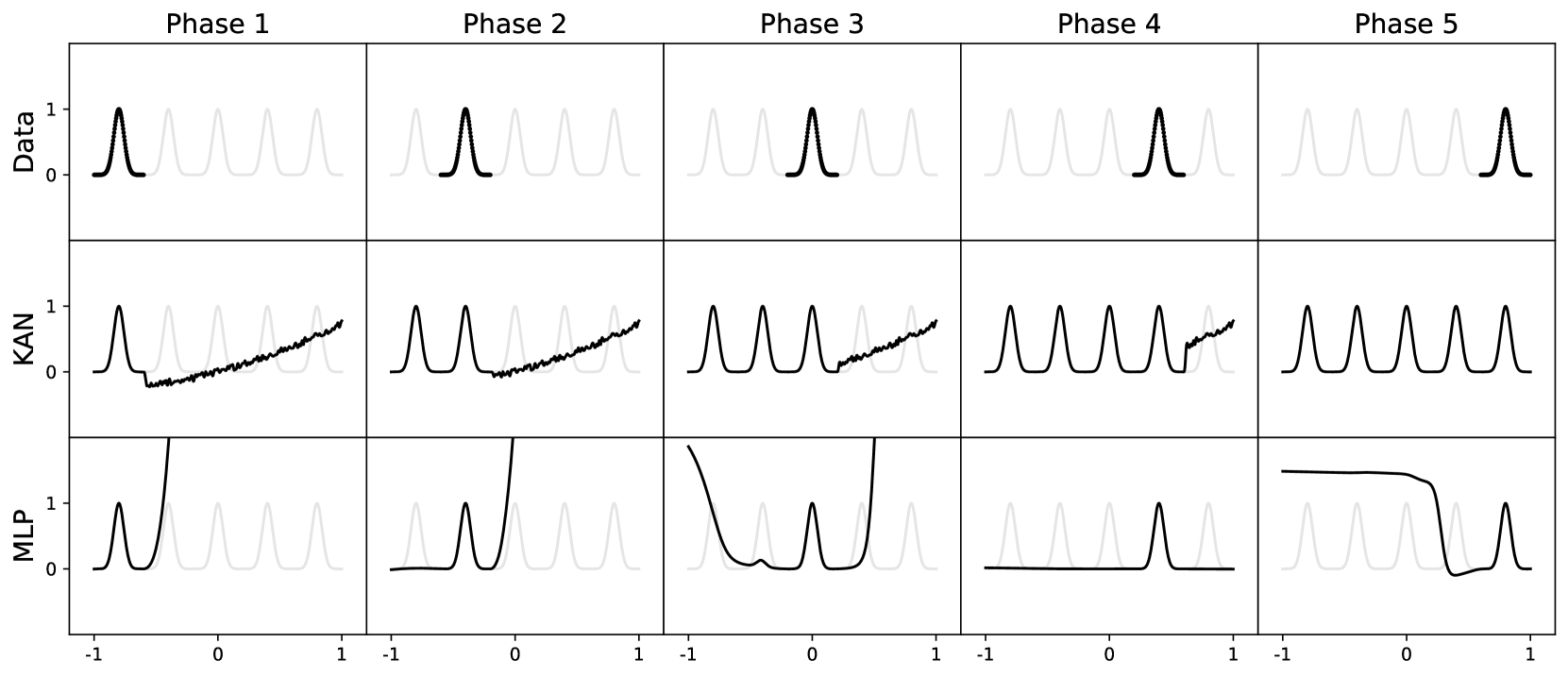
其他实验补充：

• KAN 在偏​​微分方程求解等方面具有优势，适用于数学或物理类场景
• KAN 网络可以直观地进行可视化，并且可以轻松地与人类用户交互
• 得益于 KAN 的准确性和可解释性，KAN 可能成为 AI + 科学的基础模型

本文研究团队还利用 KANs 以更小的网络和自动化方式重新复现了 DeepMind 在 2021 年登上 Nature 的纽结理论（knot theory）结果，并且以无监督的方式发现了新的结不变式关系；KAN 还可以帮助物理学家研究 Anderson 局域化（这是凝聚态物理中的一种相变）

具体细节可参阅原文，此处不再展开

后记

Kolmogorov-Arnold 网络（KAN）就像一个可以烤任何蛋糕的三层蛋糕配方，而多层感知器（MLP）是一个有不同层数的定制蛋糕。MLP 更复杂但更通用，而 KAN 是静态的，但针对一项任务更简单、更快速 ——来自 X 网友的形象比喻

设计 KAN 网络和编程时主要面向的是数学物理应用，所以在模块化/效率等等就没有太怎么考虑。目前的 KAN 在部分场景（比如大规模计算）是不如 MLP 的，KAN更适合高精度和可解释的计算和科学发现 ——Ziming Liu 作者评论

作者本人的更多解读，可参阅其在 2024 年 5 月份的直播总结

作者因为开源的代码太乱了，而被广大网友吐槽；因此有人开源了高效 KAN 的纯 PyTorch 实现；也有人用傅里叶系数取代了样条系数，提出了训练更高效的傅里叶版本 KAN

George karniadakis，PINN 网络的发明者，公开对 KAN 网络的效果提出质疑（在流体力学模拟和动力学系统上的结果存在严重错误，KAN 可能在这方面存在局限性）

KAN is just MLP 一文展示了如何将 KAN 网络改写为具有相同数量参数的、有轻微的非典型结构的普通 MLP（二者只是在计算步骤上需要一定的调整和重复）。但大家也肯定了 KAN 的创新性，尤其是 KAN 提供了 MLP 无法提供的可解释性和交互性

相关资源

• 论文在线地址
• 开源代码地址
• 本地文件地址：Liu et al_2024_KAN.pdf
• 本地Zotero地址：Liu et al_2024_KAN.pdf