1 神经网络子图
子图(subgraphs)是构建图的基础块,能够描述和区分图网络
给定图 $G=(V,E)$,可以给出 2 种方式定义子图 $G'=(V',E')$
子图的定义方式 1:节点诱导子图(Node-induced subgraph)
- 从图 $G$ 的节点集合中筛选子集来构建子图,$V'\subseteq V$
- 然后从图 $G$ 的边集合中筛选子图所有节点的对应边,$E'={(u,v)\in E|u,v\in V'}$
- 此时子图 $G'$ 被称为由节点集合 $V'$ 从图 $G$ 中诱导出的子图
子图的定义方式 2:边诱导子图(Node-induced subgraph)
- 从图 $G$ 的边集合中筛选子集来构建子图,$E' \subseteq E$
- 然后根据子图的边找到可能节点,$V'={v\in V|(v,u)\in E'\ for\ some\ u}$
- 此时子图 $G'$ 被称为由边集合 $E'$ 从图 $G$ 中诱导出的子图
两种定义方式的区别:
- 不同领域的最佳子图定义不同。比如对于化学领域,使用“节点诱导子图”定义子图能更好地描述"官能团";而知识图谱则更重视边关系中对于逻辑关系的表达,因此常常使用“边诱导子图”定义子图
- 一般来说,“节点诱导子图”由于计算成本较低,所以更常用一些;而“边诱导子图”的时间复杂度较大,但是对异常值更为鲁棒,相对不常使用
方便起见,后面将简称“节点诱导子图”为“诱导子图”,“边诱导子图”为“子图”
扩展阅读:图的同构与子图同构
2 子图模式 Motifs
Motifs:出现频率高的、比较重要的部分子图
Motifs 的作用:辅助理解图的运作方式,帮助图数据的预测
Motifs 的概念可以扩展到其他图中(比如无向图/有向图,动态图/静态图等)
Motifs 的示例:
- 生物神经网络中常存在"前馈环(Feedforward Loop)"用于消除生物噪音或处理复杂信号
- 食物链网络中常存在“平行环(Parallel Pathways)”来增加系统的冗余度,避免单一链路失效而导致整个系统的异常,从而提高了系统的稳健性
- 基因调控网络常存在“单输入模块(Single Input Module)”,确保多个基因在适当的时间和条件下被同时激活或抑制,确保系统可以对环境变化做出一致的响应
后续问题的关键在于如何定义子图的频率和重要性?
假设 $G_Q$ 是一个小图,$G_T$ 是一个目标图数据集
$G_Q$ 的图级子图频率定义:$G_T$ 中与 $G_Q$ 同构的子图数量
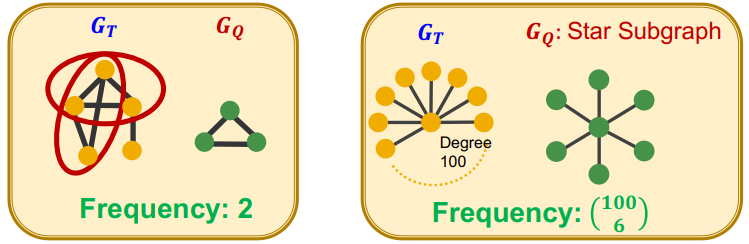
$G_Q$ 的节点级子图频率定义:
- 先在 $G_Q$ 中定义一个节点 $v$ 作为锚定节点(Anchor)
- 然后在 $G_T$ 中寻找 $G_Q$ 的同构子图,并找到锚定节点 $v$ 的对应节点 $u$
- 最终所有同构子图中节点 $u$ 的数量,就是 $G_Q$ 的节点级子图频率
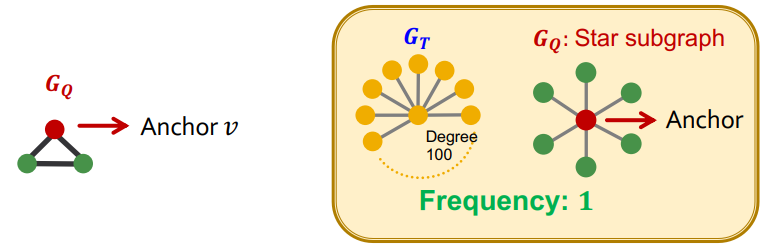
以上频率定义可以扩展到非连通图,只需把每个连通分量视为一个独立的图即可
3 子图的重要性度量
子图的重要性度量依赖随机图(null-model),简单来说:若一个子图在真实图出现的次数比在随机图中出现的次数越多,该子图的重要性就越大
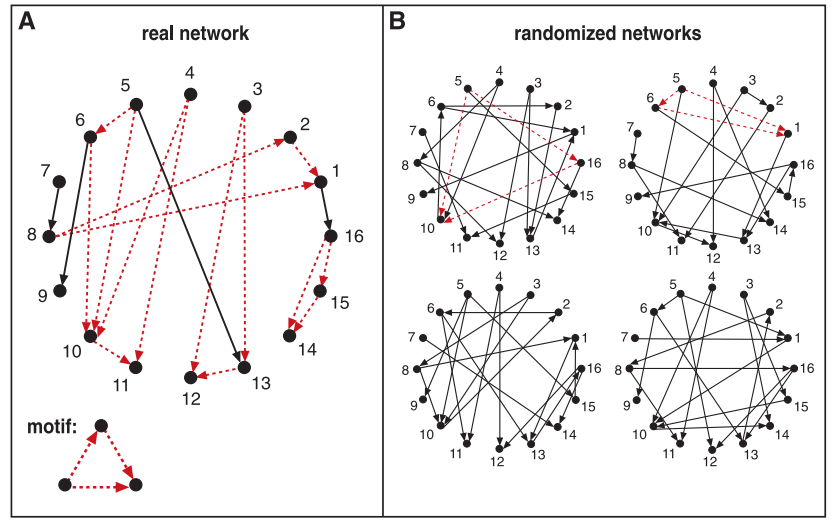
- 上图(图源)展示了一个 motif(该子图描述了三个互不相连的节点) 分别在真实图和随机图中的统计情况,该 motif 中真实图中的出现频次远高于随机图,因此重要性较高
随机图一般有两种定义方式:ER 随机图和 configuration model
- ER 随机图:先定义 $n$ 个节点,再将任意两个节点间以概率 $p$ 生成边
- Configuration model:先定义一个度数序列 $k_1,k_2,...,k_N$,然后对 $N$ 个节点进行随机配对,直到满足对应的度数要求;可能导致重边(multiple edges)和自环的情况
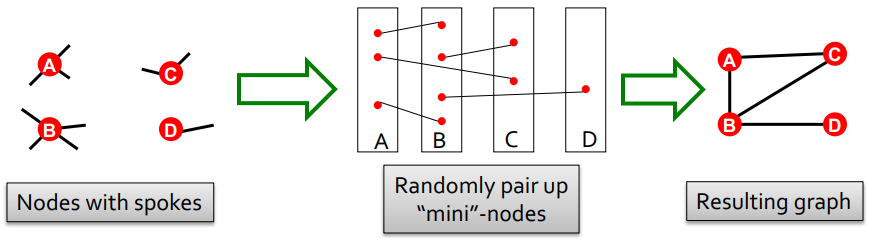
随机选择一对边(比如
A-B,C-D), 然后交换端点(A-D,C-B);该方式可以得到更多的与原图的节点度数相同的随机图;注意规避可能的重边和自环的情况
子图的重要性度量步骤:
- 给定真实图 $G^{real}$,然后进行 motifs 的计数,其中第 $i$ 个 motif 的计数为 $N^{real}_i$
- 产生$M$个随机图(尽量与真实图具有相同的统计量,比如节点数、边数、度数序列),然后进行 motifs 的计数,其中第 $i$ 个 motif 的计数为 $N^{rand}_i$
- 使用统计指标(比如 Z-score>2)衡量每种 motif 是否显著
Z-score 的计算公式: $$ Z_i=(N^{real}_i-mean(N^{rand}_i))/std(N^{rand}_i), \ \ SP_i=Z_i/\sqrt{\Sigma_j Z_j^2} $$
- $Z_i$ 可以描述第 $i$ 个 motif 的重要性;$Z_i=0$ 意味着该 motif 在真实图和随机图中出现的频次一样多,不存在显著差异,也说明该 motif 不重要
- $SP$ 是归一化的 Z-score 向量,其维度取决于 motif 的个数;$SP$ 强调了子图的相对重要性,更适合用于不同尺寸的图网络间对比(一般图规模越大,Z-score 越大)
子图的重要性度量示例:
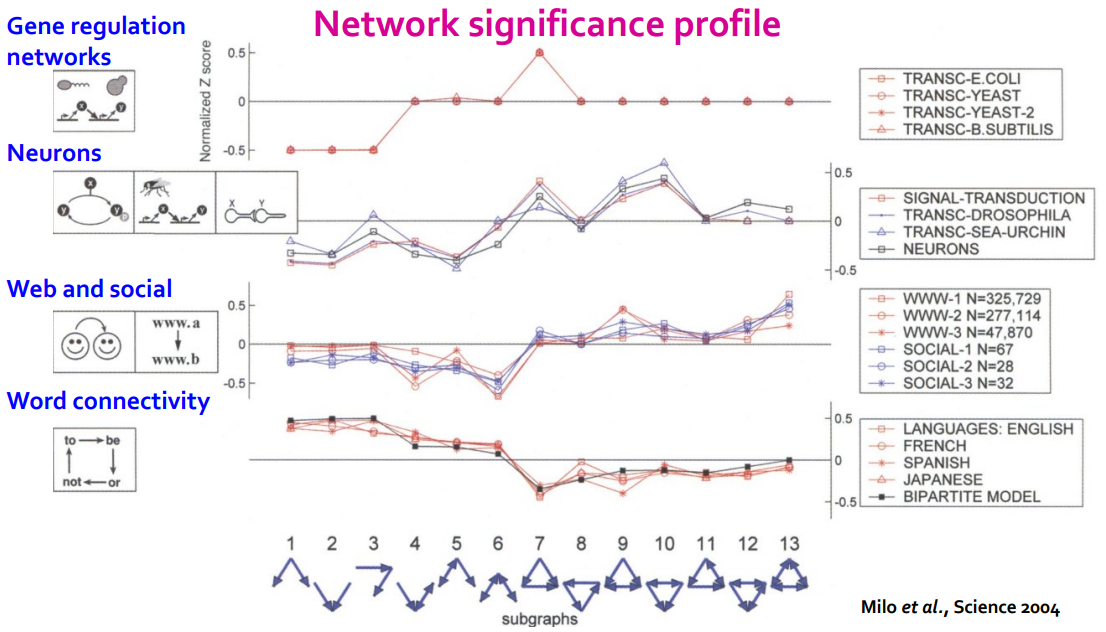
- 上图中横坐标表示不同的子图(motif),纵坐标表示不同的 $SP$ 值
- 颜色则代表领域不同,可以发现相似领域的图网络的 motif 会具有相似的 $SP$ 值
- 通过 motif 的重要性度量也能判断图网络的功能;比如子图 13 在社交网络中经常出现,这是因为你的两个亲密好友很有可能也是互相认识的
4 子图嵌入表示和匹配
子图匹配(subgraph matching)问题:如何判断给定的查询图是否为目标图的子图?
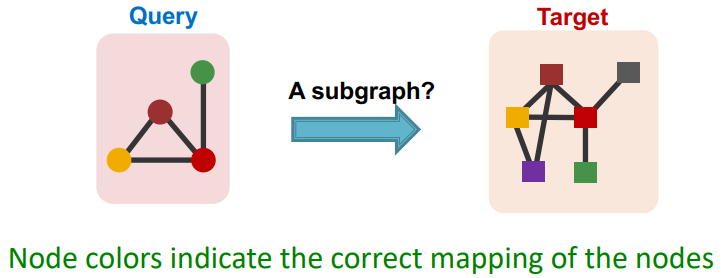
思路:利用嵌入空间捕捉子图同构的属性,然后实现 GNN 预测
具体步骤:把子图匹配问题转化为是否存在子图匹配的二元预测问题
- 遍历目标图 $G_T$ 中节点,假设当前选择的锚定节点为 $u$
- 遍历查询图 $G_Q$ 中节点,假设当前选择的锚定节点为 $v$
- 对于每个锚定节点,使用广度优先搜索找到其周围的 $k$ 阶邻
- 基于 GNN 在 $k$ 阶邻节点的子图内计算两节点对应的嵌入表示
- 根据得到的嵌入表示预测节点 $v$ 的邻居和节点 $u$ 的邻居是否同构
考虑到计算成本,一般设置节点诱导子图的最大深度为 $k=3$ 或 $5$
该方法不仅能用于判断子图匹配问题,还能找到具体的节点映射关系
有序嵌入空间(Order Embedding Space):
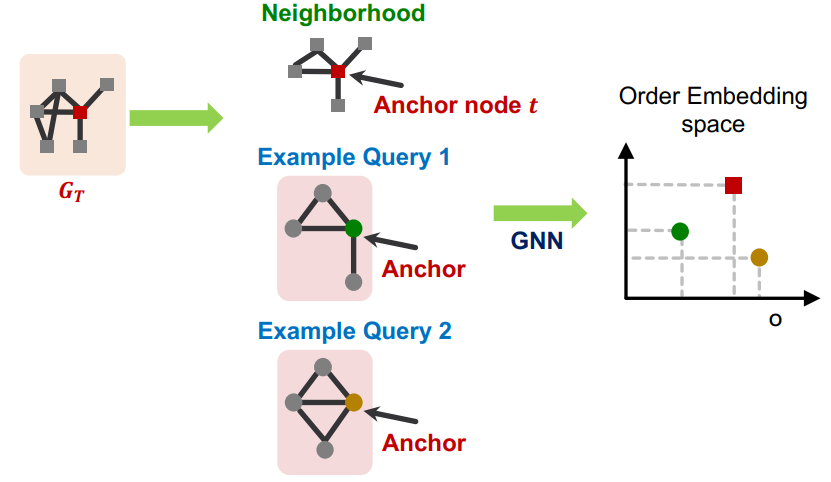
- 将嵌入表示映射到有序嵌入空间(假定向量的所有元素值都是非负的)
- 当图 A 的各个维度的元素值都小于图 B 时,意味着图 A 是图 B 的子图
- 反映到上图中,绿圆是红方块的子图,而黄圆则不是红方块的子图
顺序嵌入空间的性质
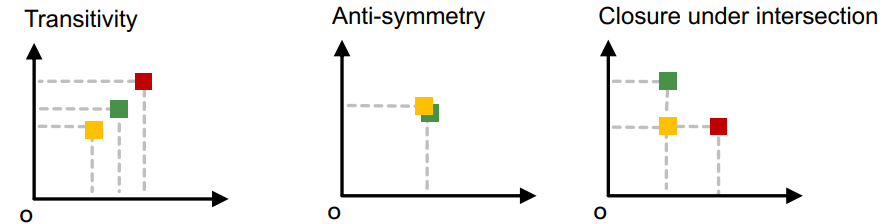
- 传递性(Transitivity):如果 A 是 B 的子图,B 是 C 的子图,那么 A 也是 C 的子图
- 反对称性(Anti-symmetry):如果 A 是 B 的子图,并且 B 是 A 的子图,则 A 同构于 B
- 交集闭包性(Closure under intersection):只含一个节点的平凡图是任何图的子图
思考:如何确保训练的 GNN 能够保留这种顺序嵌入的结构?
5 顺序嵌入 GNN 的训练
解决思路:在损失函数中添加顺序约束,确保嵌入表示能学习到相关属性
具体方法:

- 定义最大边界损失(max-margin loss),并通过损失最小化来训练 GNN
- 其中最大边界损失定义: $E(G_q,G_t)=\Sigma_{i=1}^D(max(0,z_q[i]-z_t[i]))^2$
- 当 $E(G_q,G_t)=0$,则意味着 $G_q$ 是 $G_t$ 的子图;当 $E(G_q,G_t)>0$,则不是
GNN 的训练还需要构建额外的负样本(即 $G_q$ 不是 $G_t$ 子图的情况)
从图数据集 $G$ 中生成查询图 $G_Q$ 和目标图 $G_T$:
- 首先从 $G$ 中随机选择锚定节点 $v$ 及其所有的 $k$ 阶邻域节点,构成 $G_T$
- 对于正样本的合成,每次从锚定节点 $v$ 的所有邻域节点中筛选 10%的节点,重复 $k$ 次后(已筛选到的节点不再纳入抽样过程),得到节点诱导子图构成的 $G_Q$
- 对于负样本的合成,对正样本 $G_Q$ 中的节点/边进行随机的添加或删除
每个训练迭代过程,都会进行样本的合成,避免模型出现过拟合的问题
已训练好的模型在新图上进行推理:
- 给定查询图和目标图,遍历每个节点并分别作为锚定节点
- 使用 GNN 计算两个锚定节点的对应嵌入表示,并计算 $E(G_q,G_t)$
- 当 $E(G_q,G_t)<\epsilon$ ($\epsilon$ 是超参数)时,说明查询图是目标图的子图
对于满足顺序约束的嵌入空间,能根据节点的相对位置来判断子图同构的情况
6 SPMiner:频繁子图的挖掘
输入信息:给定目标图 $G_T$ 和子图的尺寸参数 $k$,所需的子图数量 $r$
目标输出:在 $G_T$ 中统计出现频次最高的 $r$ 个尺寸为 $k$ 的子图
初步思路:先迭代所有大小为 $k$ 的子图,再统计每类子图的出现频次
问题:确定特定子图是否在图中存在(子图同构),是一个计算成本很高的事情;而统计频繁子图则是在此基础上的再进行组合运算(指数级);因此该问题是一个 1_study/math/NP-Hard 问题
优化思路:使用表示学习来解决该问题
- 使用 GNN 来直接预测子图同构问题(二分类)
- 将指数级的组合运算转化为顺序嵌入空间的搜索问题
SPMiner:识别频繁主题的神经模型
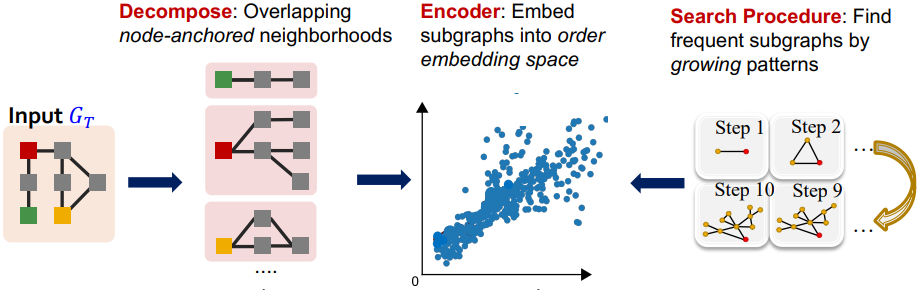
- 分解(Decompose),遍历目标图 $G_T$ 的节点,并分别构建节点诱导子图
- 编码(Encoder):使用训练好的 GNN 网络将子图转化为顺序嵌入空间的表示
- 搜索过程(Search Procedure):基于生长模式寻找频繁子图,并估计出现频率
步骤 1 和步骤 2 和 子图嵌入表示和匹配一节内容是一致的
搜索过程(Search Procedure)细节:
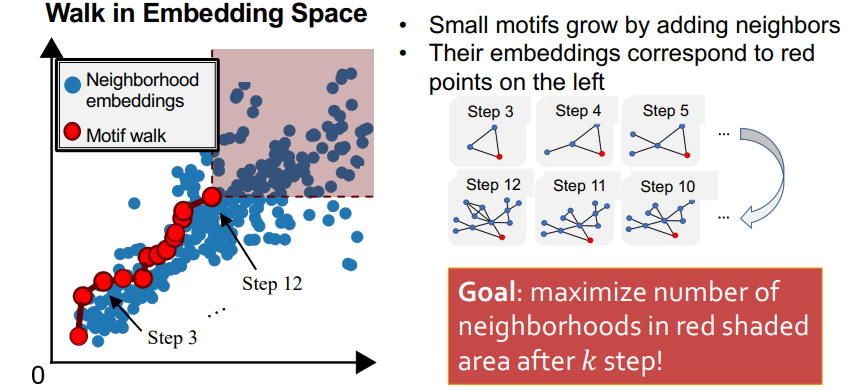
- 首先随机选择一个节点 $u$(交集闭包性(Closure under intersection):只含一个节点的平凡图是任何图的子图),并构建子图 $S={u}$
- 在每次迭代过程中,基于贪心算法找到子图 $S$ 中某一节点的新邻居,添加到 $S$ 中;贪心算法的目标是更新后的 $S$ 的右上区域(对应上图红色方形阴影区域)内的节点数最大化
- 重复迭代 $k$ 次后,即可得到一个满足预期尺寸的频繁子图,其右上区域内的节点数对应着该频繁子图出现频率的统计
该方法利用了顺序嵌入空间的特性,实现了频繁子图的高效发现和计数
SPMiner 的性能评估:
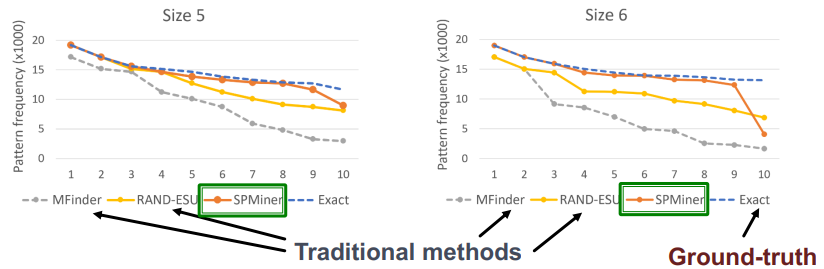
- SPMiner 可以识别出频繁子图 Top 10 中的前 9/8 个,并且识别频率接近真实值
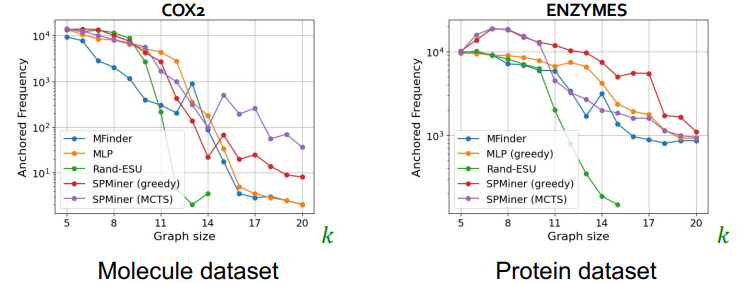
- 在查找大的 motif 时(k 值在 10~20 之间),SPMiner 也明显要优于传统方法