中文标题:时间关系排名股票预测
英文标题:Temporal Relational Ranking for Stock Prediction
发布平台:Transactions on Information Systems
ACM Transactions on Information Systems
发布日期:2019-04-30
引用量(非实时):308
DOI:10.1145/3309547
作者:Fuli Feng, Xiangnan He, Xiang Wang, Cheng Luo, Yiqun Liu, Tat-Seng Chua
文章类型:journalArticle
品读时间:2024-01-10 15:57
1 文章萃取
1.1 核心观点
本文提出了一个名为关系股票排名(RSR)的端到端框架来解决股票排名问题。该框架先通过 LSTM 模型从股票历史时序数据中捕获顺序依赖性并学习股票顺序嵌入,然后借助时态图卷积(TGC)以时间敏感的方式考虑股票关系来修改顺序嵌入。最后将顺序嵌入和关系嵌入的串联输入到全连接层以获得股票的排名分数。
实验分析表明,相比于其他算法本文提出的 RSR 方法具备性能优越性。本文模型在纽约证券交易所和纳斯达克分别实现了 98% 和 71% 的平均回报率
1.2 综合评价
- 时序图卷积将 LSTM 的隐藏层引入 GCN 的邻接矩阵,实现二者的有效结合
- 行文清晰,实验充分,代码开源;验证了模型中每一个组件的有效性
- SRS 的框架效率存疑,尤其是在知识图较大或者嵌入维度较多的情况下
1.3 主观评分:⭐⭐⭐⭐⭐
2 精读笔记
主流的股票预测解决方案的主要缺点:
- 模型严重依赖指标的选择,这通常是手动完成的,依赖专门的金融知识
- 假设的随机过程并不总是与现实世界中的波动性股票兼容
- 这些模型只能考虑少数指标,推理复杂度通常随着指标数量呈指数级增长
- 通常将股票视为彼此独立,而忽略股票之间的关系
2.1 RSR 框架细节
RSR(Relational Stock Ranking)框架概览:
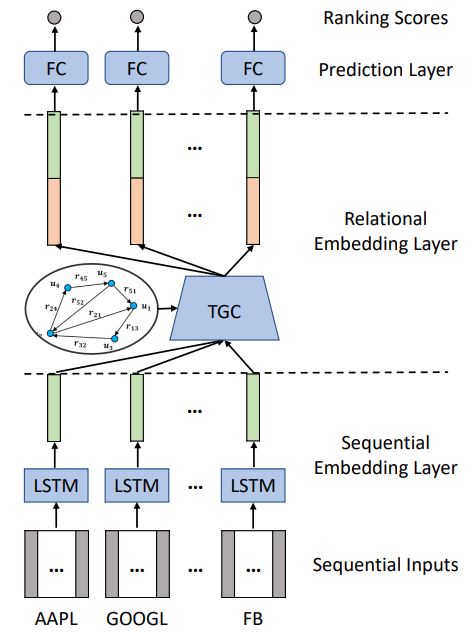
- 顺序嵌入层(Sequential Embedding Layer),借助 LSTM 依次捕捉每只股票历史价格中的长期依赖性(年报发布/利率变化/价值回归),最后的隐藏状态为股票的顺序嵌入
- 关系嵌入层(Relational Embedding Layer),先根据股票的行业信息和 wiki 信息(创始人、股权归属、上下游关系等 5 种一阶关系和 53 种和二阶关系)构建知识图,之后借助时间图卷积根据股票关系修改顺序嵌入,以时间敏感(动态)的方式生成关系嵌入
- 预测层(Prediction Layer),将顺序嵌入和关系嵌入提供给全连接层以预测每只股票的排名分数
结合了点回归损失和成对排名感知损失的目标函数: $$ l(\mathbf{\hat{r}}^{t+1},\mathbf{r^{t+1}})=\left|\mathbf{\hat{r}}^{t+1}-\mathbf{r^{t+1}}\right|^2+\alpha\sum_{i=0}^N\sum_{j=0}^Nmax(0,-(\mathbf{\hat{r_i}}^{t+1}-\mathbf{\hat{r_j}}^{t+1})(r_i^{t+1}-r_j^{t+1})), $$
- 其中 $\hat{r}^{t+1},\mathbf{r^{t+1}}$ 分别表示真实分数和预测排名分数;$\alpha$ 是平衡两个损失项的超参数
- 第一个回归项惩罚真实分数和预测分数之间的差异;第二项是成对最大边际损失(pair-wise max-margin loss ),鼓励股票对的预测排名得分与真实情况一致
细节 1:时序图卷积的实现:
- 给定 $N$ 只股票及其顺序嵌入 $\mathbf{E^{t}}\in\mathbb{R}^{N\times U}$(即顺序嵌入层的输出)及其多热二元关系编码(multi-hot binary relation encodings) $\mathcal{A}\in\mathbb{R}^{N\times N\times K}$,时序图卷积的目标是学习根据关系信息进行编码调整后的嵌入 $\bar{\mathrm{E}^{\mathrm{t}}}\in\mathbb{R}^{N\times U}$
- 对于股票 $i$ 在 $t$ 时刻的最终编码 $\bar{e^t_i}$ 可表示如下:
$$ \bar{e_i^t}=\sum_{{j|sum(a_{ji})>0}}\frac{g(a_{ji},e_i^t,e_j^t)}{d_j}e_j^t, $$
- 其中 $a_{ji}$ 是一个多热二元向量,其中每个元素表示股票 $i$ 和股票 $j$ 之间是否存在特定类型(共有 $K$ 种类型)的关系;$sum(a_{ji})$ 是关系向量 $a_{ji}$ 中所有元素的总和,$sum(a_{ji})>0$ 表示股票 $i$ 和股票 $j$ 之间至少存在一种关系
- $d$ 是满足条件 $sum (a_{ji})>0$ 的股票数量,用于关系强度的修正(取矩阵)
- $g$ 是一种映射函数,被称为关系强度函数;函数 $g$ 会根据关系向量和对应两种股票的顺序嵌入表示,来评估两只股票间的关系强度;由于顺序嵌入来自具备时间感知的 LSTM,因此最终的关系强度也会是时间敏感的
假设关系强度函数 $g$ 恒等于 1,时序图卷积将弱化为普通图卷积 GCN
所以时序图卷积的时间感知来自对普通 GCN 中邻接矩阵的改造,即使用具备时间敏感的关系强度作为邻接矩阵的权重;但需要注意的是,在普通 GCN 中邻接矩阵是固定不变的;因此需要额外的代码开发来单独实现时序图卷积
细节 2:关系强度函数的 2 种实现:
- 显式建模(组成函数的两项都可以直接解释):
$$ g(a_{ji},\mathbf{e_i^t},\mathbf{e_j^t})=\underbrace{\mathbf{e_i^{t}e_j^t}}_{\text{similarity}}\times\underbrace{\phi(\mathbf{w}^Ta_{ji}+b)}_{\text{relation importance}}, $$
- 第一项衡量两只股票在当前时间步长之间的相似性;两只股票越相似(内积),它们的关系就越有可能在不久的将来影响它们的价格
- 第二项是关系的非线性回归模型,其中 $w$ 中的每个元素一般表示关系的权重
- 隐式建模(由参数隐式捕获关系强度):
$$ g(\mathbf{a_{ji}},\mathbf{e_{i}^{t}},\mathbf{e_{j}^{t}})=\phi(\mathbf{w}^{T}[\mathbf{e_{i}^{t}}^{T},\mathbf{e_{j}^{t}}^{T},\mathbf{a_{ji}}^{T}]^{T}+b) $$
- 将顺序嵌入和关系向量输入到全连接层中以估计关系强度
- 使用 softmax 函数对输出进行归一化,也赋予关系强度更多的非线性
2.2 实验结果与分析
股票价格时序数据概述:
| Market | Stocks# | Training Days#<br><br>01/02/2013<br>12/31/2015<br> | Validation Days#<br><br>01/04/2016<br>12/30/2016 | Testing Days#<br><br>01/03/2017<br>12/08/2017 |
|---|---|---|---|---|
| NASDAQ | 1,026 | 756 | 252 | 237 |
| NYSE | 1,737 | 756 | 252 | 237 |
知识图数据概述:
| - | Sector-Industry Relation | Sector-Industry Relation | Wiki Relation | Wiki Relation |
|---|---|---|---|---|
| - | Relation Types# | Relation Ratio (Pairwise) | Relation Types# | Relation Ratio (Pairwise) |
| NASDAQ | 112 | 5.00% | 42 | 0.21% |
| NYSE | 130 | 9.37% | 32 | 0.30% |
交易策略说明:
- 当日买入排名最高的股票,然后在次日卖出(均使用收盘价)
- 每日交易金额一致,以方便公平比较;忽略交易成本
三个评价指标:均方误差(MSE)、平均倒数排名(MRR)和累积投资回报率(IRR)
评价所考虑的模型列表:
- Rank_LSTM:在 RSR 的基础上删除关系嵌入层,即忽略股票的关系信息
- GBR(Graph-based ranking):将图正则化项添加到 Rank_LSTM 的损失函数中
- GCN:使用 GCN 层替换 RSR 中的 TGC(时序图卷积)层
- RSR_E:在 TGC 中具有显式建模的 RSR
- RSR_I:在TGC 中采用隐式建模的RSR
模型对比(评估顺序嵌入层的有效性):
| NASDAQ 纳斯达克 | NASDAQ 纳斯达克 | NASDAQ 纳斯达克 | NYSE 纽约证券交易所 | NYSE 纽约证券交易所 | NYSE 纽约证券交易所 | |
|---|---|---|---|---|---|---|
| MSE (e-4) | MRR (e-2) | IRR | MSE (e-4) | MRR (e-2) | IRR | |
| SFM | 5.2±0.577 | 2.33±1.07 | -0.25±0.52 | 3.81±0.93 | 4.82±0.495 | 0.49±0.47 |
| LSTM | 3.81±0.022 | 3.64±1.04 | 0.13±0.62 | 2.31±0.0143 | 2.75±1.09 | -0.90±0.73 |
| Rank_LSTM | 3.79±0.0111 | 4.17±0.75 | 0.68±0.60 | 2.28±0.0116 | 3.79±0.882 | 0.56±0.68 |
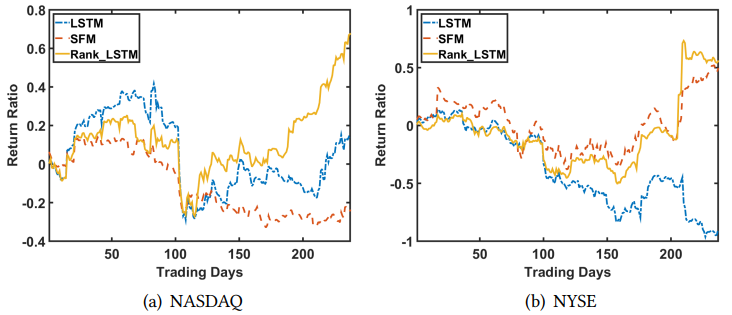
- Rank_LSTM 在两个市场上均优于 SFM 和 LSTM,并且在性能方面有很大改进
- Rank_LSTM 在 NYSE 的 MRR 比 SFM 差;原因可能是模型在回报率和顺序预测间的权衡
- LSTM 在纽约证券交易所市场的 IRR 表现较差;LSTM 在验证集的表现与测试集差异较大
模型对比(评估行业关系信息引入的有效性):
| NASDAQ 纳斯达克 | NASDAQ 纳斯达克 | NASDAQ 纳斯达克 | NYSE 纽约证券交易所 | NYSE 纽约证券交易所 | NYSE 纽约证券交易所 | |
|---|---|---|---|---|---|---|
| MSE (e-4) | MRR (e-2) | IRR | MSE (e-4) | MRR (e-2) | IRR | |
| Rank_LSTM | 3.79±0.0111 | 4.17±0.75 | 0.68±0.60 | 2.28±0.0116 | 3.79±0.882 | 0.56±0.68 |
| GBR | 58±12 | 4.46±0.520 | 0.57±0.29 | 2.29±0.0202 | 3.43±0.626 | 0.68±0.31 |
| GCN | 3.80±0.0224 | 3.45±0.836 | 0.24±0.32 | 2.27±0.0013 | 5.01±0.556 | 0.97±0.56 |
| RSR_E | 3.82±0.0269 | 3.16±0.345 | 0.20±0.22 | 2.29±0.0277 | 4.28±0.618 | 1.00±0.58 |
| RSR_I | 3.80±0.0079 | 3.17±0.509 | 0.23±0.27 | 2.26±0.0053 | 4.51±0.241 | 1.06±0.27 |
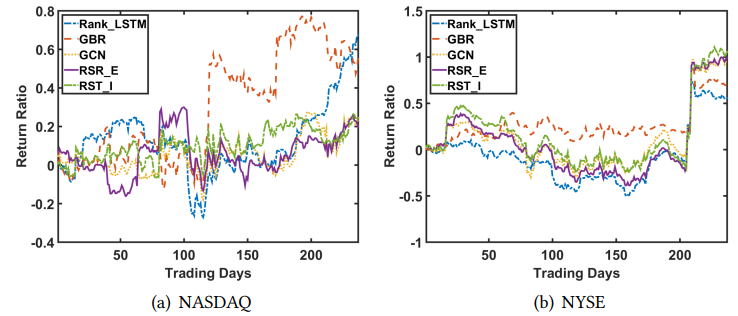
- 与纳斯达克相比,考虑行业关系更有利于纽约证券交易所的股票排名;纳斯达克波动性更大,容易受短期因素主导,而行业关系更多地反映了股票间的长期相关性
- 在 NYSE,所有考虑股票关系的方法(即 GBR、GCN、RSR_E 和 RSR_I)均优于 Rank_LSTM
- RSR_E 和 RSR_I 实现了对 GCN 和 GBR 的改进,该结果验证了所提出的时间图卷积的有效性
- 不同评估指标的表现也不一致;模型实现更好的 IRR 可能会实现次优的 MSE 和 MRR
模型对比(评估 Wiki 关系信息引入的有效性):
| NASDAQ 纳斯达克 | NASDAQ 纳斯达克 | NASDAQ 纳斯达克 | NYSE 纽约证券交易所 | NYSE 纽约证券交易所 | NYSE 纽约证券交易所 | |
|---|---|---|---|---|---|---|
| MSE (e-4) | MRR (e-2) | IRR | MSE (e-4) | MRR (e-2) | IRR | |
| Rank_LSTM | 3.79±0.0111 | 4.17±0.75 | 0.68±0.60 | 2.28±0.0116 | 3.79±0.882 | 0.56±0.68 |
| GBR | 3.80±0.0024 | 3.32±0.45 | 0.33±0.34 | 2.26±0.004.2 | 3.64±0.535 | 0.65±0.27 |
| GCN | 3.79±0.0097 | 3.24±0.321 | 0.11±0.06 | 2.26±0.0066 | 3.99±1.03 | 0.74±0.30 |
| RSR_E | 3.80±0.0072 | 3.94±0.815 | 0.81±0.85 | 2.29±0.0277 | 4.28±0.618 | 0.96±0.47 |
| RSR_I | 3.79±0.0066 | 4.09±0.518 | 1.19±0.55 | 2.26±0.0137 | 4.58±0.555 | 0.79±0.34 |
- 在所有情况下,我们提出的 RSR_E 和 RSR_I 都实现了最佳性能
- 所有考虑 Wiki 关系的方法均优于 Rank_LSTM,并具有显着改进
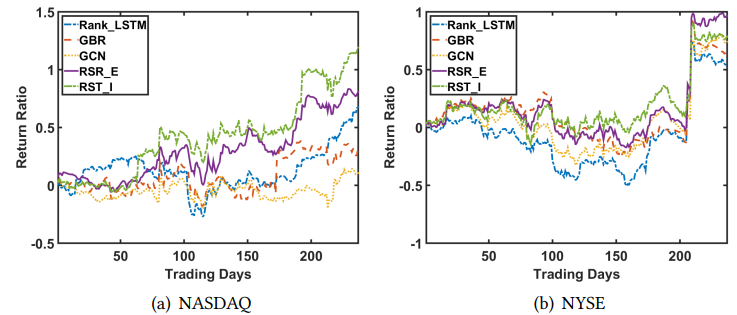
不同板块的回测对比