1 推荐系统的任务与评价
推荐系统可以建模为二分图(bipartite graph)
- 具有两种类型的节点——用户(user)和项(item)
- 边用于连接用户和项,表示二者间的互动(比如点击、购买或评论)
任务:给定历史图,预测每个用户未来将产生的交互项(链接预测问题)
前置知识:推荐排序模型评价指标
基于嵌入表示的推荐系统建模思路
- 对于每一个用户 $u$,基于编码器生成对应的用户嵌入表示
- 对于每一个可交互项 $v$,基于编码器生成对应的项嵌入表示
- 构建评分函数 $f_{\theta}(u,v)$ 来评估用户 $u$ 和项 $v$ 产生交互的可能性
- 训练目标是追求在可见的用户-项的交互上实现较高的 recall@K
思考: recall@K 不可微分,需要替代的损失函数指导梯度更新
推荐系统的基本思想:协同过滤
- 系统通过搜集相似用户的偏好,为用户进行项的推荐
- 相似的用户往往更喜欢相似的项,而嵌入模型能很好地捕获相似性
2 推荐系统的损失函数
考虑使用常见的二元损失作为损失函数? $$ -\frac1{|E|}\sum_{(u,v)\in E}\log\left(\sigma(f_\theta(\boldsymbol{u},\boldsymbol{v}))\right)-\frac1{|E_{\mathrm{neg}}|}\sum_{(u,v)\in E_{\mathrm{neg}}}\log\left(1-\sigma(f_\theta(\boldsymbol{u},\boldsymbol{v}))\right) $$
- 其中 $E$ 表示边的正样本集合,无真实交互的负样本边集合为 $E_{neg}$
- 二元损失会追求正样本边更高的得分,而负样本边更低的得分
- 问题 1,负样本边有可能是潜在的可交互项,不应该一律否定
- 问题 2,二元损失同时考虑了所有用户的边信息,是非个性化的
recall@K 的本质是个性化的,需要为每个用户进行单独定义
贝叶斯个性化排名(BPR)损失: $$ \mathrm{Loss}(u^\star)=\frac1{|E(u^\star)|\cdot|E_{\mathrm{neg}}(u^\star)|}\sum_{(u^\star,v_{\mathrm{pos}})\in E(u^\star)}\sum_{(u^\star,v_{\mathrm{neg}})\in E_{\mathrm{neg}}(u^\star)}-\log\left(\sigma\left(f_\theta(\boldsymbol{u}^\star,\boldsymbol{v}_{\mathrm{pos}})-f_\theta(\boldsymbol{u}^\star,\boldsymbol{v}_{\mathrm{neg}})\right)\right) $$
- 对于每一个用户 $u^\star$,需要从正样本边集合 $E$ 中筛选出以 $u^\star$ 为起始节点的边子集 $E(u^\star)$,从负样本边集合 $E_{neg}$ 中筛选出以 $u^\star$ 为起始节点的边子集 $E_{neg}(u^\star)$
- BPR 损失是一种个性化损失,可以与训练指标 recall@K 更好地保持一致性
最终模型训练的 BPR 损失函数其实是所有用户的 BPR 损失的均值: $$ \mathrm{BPR\ Loss}=\frac{1}{|U|}\Sigma_{u^\star\in U}\mathrm{Loss}(u^\star) $$
在实际的小批量训练时,会对用户子集 $U_{mini}$ 中的每个用户采样一个正样本项 $v_{pos}$ 和一组负样本项集合 $V_{neg}={v_{neg}}$,其对应的小批量损失如下: $$ \frac1{|U_{\mathrm{mini}}|}\sum_{u^{\star}\in U_{\mathrm{mini}}}\frac1{|V_{\mathrm{neg}}|}\sum_{v_{\mathrm{neg}}\in V_{\mathrm{neg}}}-\log\left(\sigma\left(f_{\theta}(u^{*},v_{\mathrm{pos}})-f_{\theta}(u^{*},v_{\mathrm{neg}})\right)\right) $$
3 NGCF 神经图协同过滤
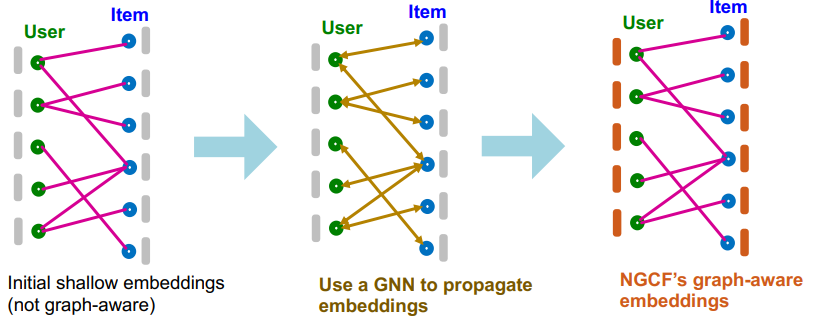
- 初始化的浅层编码器(shallow embeddings)只能借助损失函数,隐式地包含部分图结构信息,而不是显式地捕获到图结构信息(尤其是高阶图结构)
- 借助 GNN 则可以根据邻近节点的嵌入迭代更新节点嵌入,聚合捕获高阶图结构
- 经过 K 轮迭代后,最终的节点嵌入表示(user 和 item)将包含丰富的图结构信息;NGCF 则根据函数 $f_{\theta}(u,v)=u^Tv$ 来计算给定交互项的推荐得分
节点嵌入的第 $k$ 次更新(具体原理之前的 GNN 提到过,不再赘述): $$ \begin{align} h_{v}^{(k+1)}=\mathrm{COMBINE}\left(\boldsymbol{h}_{v}^{(k)},\mathrm{AGGR}\left( \left\{\boldsymbol{h}_{u}^{(k)}\right}_{u\in N(v)}\right)\right) \ \\ \\\boldsymbol{h}_{u}^{(k+1)}=\mathrm{COMBINE}\left(\boldsymbol{h}_{u}^{(k)},\mathrm{AGGR}\left( \left\{\boldsymbol{h}_{v}^{(k)}\right}_{v\in N(u)}\right)\right) \end{align} $$
- 其中
AGGR函数可以考虑均值计算MEAN() COMBINE函数可以考虑ReLU(Linear(Concat(x,y))),
NGCF 的参数分析:
- 假设节点数为 $N$,浅层嵌入表示的维度为 $D$
- NGCF 的参数组成:嵌入表示相关参数 $O(ND)$ 和 GNN 的参数 $O(D^2)$
- 当 $N>>D$ 时,NGCF 的绝大部分参数都处于嵌入表示部分
- 由此可知,GNN 部分的参数对于 NGCF 的模型表现影响不大
改进策略:继续简化 GNN 部分的参数来提高性能
4 LightGCN 轻量版 NGCF
由前文可知,单层 GCN 的公式如下: $$ H^{(l+1)}=\sigma(\tilde{D}^{-1/2}\tilde{A}\tilde{D}^{-1/2}H^{(l)}W^{(l)}) $$
- 其中 $\tilde{A}$ 表示添加了自环(自连接)的邻接矩阵 $A$
LightGCN 的输入可表示如下:
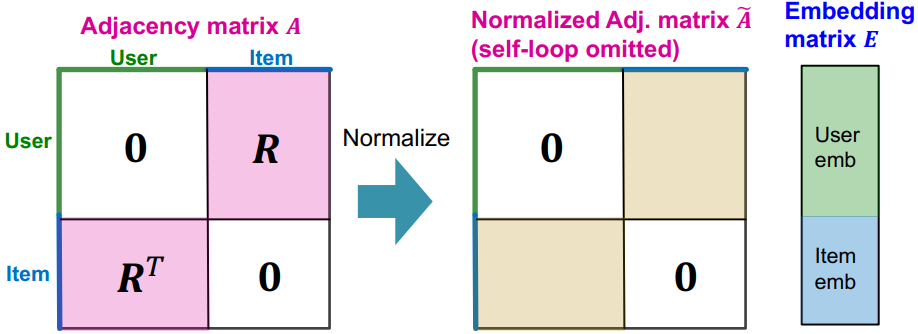
- 对于 LightGCN ,节点不需要考虑自环(自连接)的情况
- 其中 $\widetilde{A}$ 表示归一化后的邻接矩阵:$\widetilde{A}=D^{-1/2}AD^{-1/2}$
- 初始化的嵌入表示矩阵 $E$ ,会在训练过程中不断更新参数
LightGCN 通过消除非线性来简化 GCN,其对应 GNN 公式如下:
$$
E^{(K)}=\widetilde{A}E^{(K-1)}W^{(K-1)}=\widetilde{A}^KE(W^{(0)}...W^{(K-1)})
$$
LightGCN 考虑通过扩散机制,聚合所有层的嵌入均值来得到最终的节点嵌入表示:
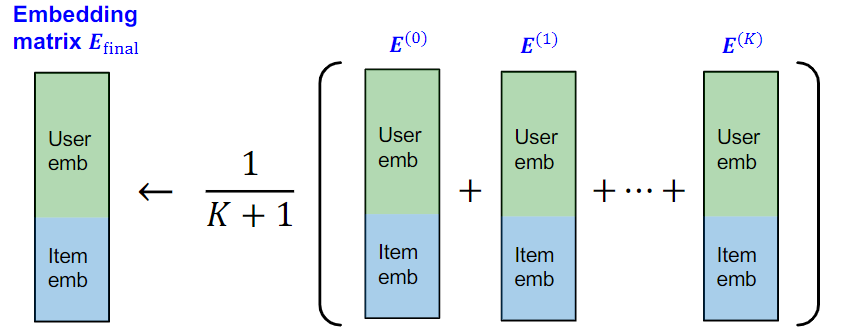
此处扩散机制的计算较为简单,可以修改优化不同层的聚合权重
类似于 NGCF,LightGCN 也根据函数 $f_{\theta}(u,v)=u^Tv$ 来计算给定交互项的推荐得分;其中用户和项的嵌入表示均来自最终的嵌入表示矩阵 $E_{final}$
LightGCN 的分析:
- 不考虑自环(自连接)的情况,最终嵌入使用所有层嵌入的平均值
- 去除了非线性变换,直接鼓励用户和项的最终嵌入表示的相似度计算
- 保留 NGCF 优势的同时简化了 GNN 的可学习参数,最终表现优于 NGCF
- 由于额外的扩散机制(涉及矩阵向量乘法),计算成本也高于 NGCF
5 PinSAGE 大规模图的推荐
PinSAGE 的特点:
- 统一视觉、文本和图结构信息;能做到相对实时的更新(几秒钟)
- 首次实现了大规模图的推荐和应用,在 Pinterest 内得到了广泛采用
Pinterest,一款基于图片的流行社交软件,其中文名称是拼趣
PinSAGE 的目标:为包含数十级大规模图生成用于推荐的嵌入表示

PinSAGE 的改进 1:
- 在贝叶斯个性化排名(BPR)损失计算中,使用共享的负样本改善性能
- 每个小批次的训练样本,共享同一组负样本,节省负样本的嵌入表示计算
PinSAGE 的改进 2:
- 工业推荐场景需要实现更精细的预测,从数十亿项中为每个用户推荐 10~100 个项
- 因此需要在训练过程中逐渐增加复杂的负样本来改善模型的预测,即 Hard Negatives
 Hard Negatives 的细节:
Hard Negatives 的细节:
- 以用户节点为起点,对项节点进行重复随机游走;然后按照访问次数对项进行降序排列,随机抽取排名中不高也不低的项(比如排名在 2000~5000 之间)
- 该方法抽样得到的项与用户接近,但又不是特别近,很适合作为 Hard Negatives
- 最终的负样本集合还会包含共享的负样本组,而 Hard Negatives 则会逐渐增加(具体来说,对于第 $n$ 次迭代,最终的负样本会纳入 $n-1$ 个 Hard Negatives)
- 负样本的采样策略:筛选负样本使得样本对的距离分布尽量满足 $U[0.5,1.4]$
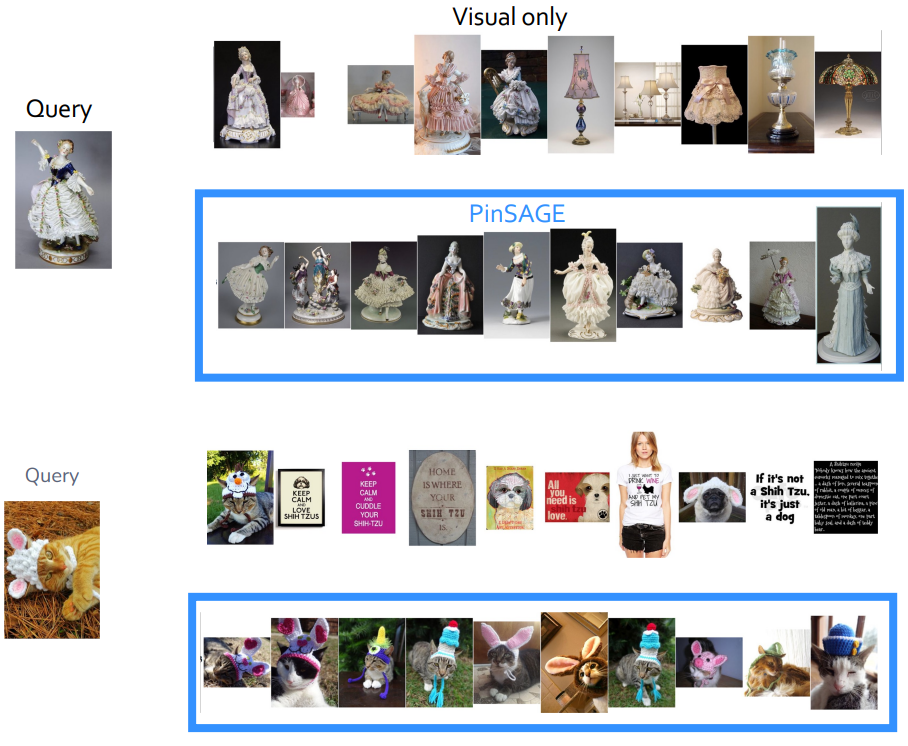
PinSAGE 的最终效果示例(确实还不错,但对于社交类 APP 来说有些同质化了):