前置知识:因果效应评估_配平法、因果效应评估_异质性 、因果效应评估_元学习
双重机器学习
双重机器学习 (Double Machine Learning, DML):利用机器学习强大的预测能力,先剔除 X 对 T 的影响,再剔除 X 对 Y 的影响,最后看残差之间的关系。
DML 的实现过程:
- 先构建回归模型 $M_{y}$,该模型能根据特征 $X$ 来估计结果 $Y$
- 再构建回归模型 $M_{t}$,该模型能根据特征 $X$ 来估计干预 $T$
- 计算两个模型的残差:$\tilde{Y} = Y - M_y(X)$,$\tilde{T} = T - M_t(X)$
- 利用干预残差来回归预测结果残差:$\tilde{Y} = \alpha + \tau \tilde{T}$
- 最终得到的回归系数 $\tau$ 就是因果效应的估计值(ATE)
$M_{t}$ 也称为去偏模型,主要用于消除干预效应中的偏差;其模型的残差 $\tilde{T}$ 与 $X$ 是正交的,即去偏差后的干预 $\tilde{T}$ 不能用 $X$ 解释
$M_{y}$ 也称为去噪模型,主要用于消除所有由 $X$ 引起的偏差;$X$ 引起的可解释方差被剔除后,即得到了模型的残差 $\tilde{Y}$ ,该残差的噪声较少,能容易发现因果关系
异质性 DML
当存在异质性因果效应时,可以通过调整残差回归方程来估计 CATE: $$ \tilde{Y_i} = \alpha + \beta_1 \tilde{T_i} + \pmb{\beta}_2 \pmb{X_i} \tilde{T_i} + \epsilon_i $$
R-Learner 在 DML 的基础上通过定义了一个通用损失函数(R 损失),来实现用任意模型一步到位的 CATE 建模预测,其中 R 损失函数定义如下: $$ \hat{L}_n(\tau(x)) = \frac{1}{n} \sum^n_{i=1}\left( \tilde{Y}_i - \tau(X_i) \tilde{T}_i \right)^2= \frac{1}{n} \sum^n_{i=1} \tilde{T}_i^2 \left(\frac{\tilde{Y}_i}{\tilde{T}_i} - \tau(X_i)\right)^2 $$
- 设置样本权重为 $\tilde{T}^2$,模型的预测目标为 $\tilde{Y}_i / \tilde{T}_i$;即可将异质性因果效应的评估建模,转化为常见的非参数机器学习,
DML 的分析
- 作为一种通用的因果效应评估方法,既直观又严谨;既适用于连续数据也适用于离散数据;但是 DML 的最终效果取决于所选择的模型类型
- DML 的效应估计是非线性 CATE 的局部线性近似,因此其结果很难外推到其他存在较大差异的干预情况,也不适用于干预效应存在非线性的情况
- 当 $M_{y}$ 模型过拟合或捕捉到了 $T$ 和 $Y$ 的因果关系时,$M_{y}$ 模型的残差 $\tilde{Y}$ 会小于预期,后续的残差回归也会缺少相关信息,进而导致 ATE 的方差偏高;通过交叉预测,可以有效改善 DML 的残差回归问题:
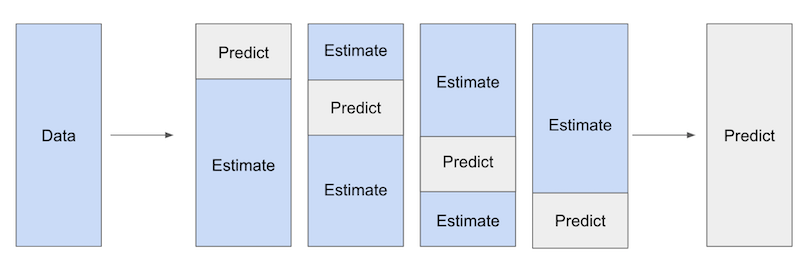
- 将数据进行 K 等分,每次使用 K-1 份数据进行训练,然后计算第 K 份数据的残差
- 汇总 K 次计算的残差结果,在通过残差回归来估计最终的干预效应值