前置知识:因果效应评估_准实验、因果效应评估_异质性 、双重机器学习 DML
双向固定效应
双向固定效应(Two Way Fixed Effect,TWFE)
- 作为双重差分法 DID 的一种常见回归模型实现方式
- TWFE 假设干扰效应是常量,并引入个体/时间的固定效应
- 对于不同组的干预时间相同的情况,TWFE 和 DID 是等价的
当出现不同组的干预时间不同的情况,即错位实施(Staggered Adoption),TWFE 对干预效应的评估容易存在偏差,尤其是干预效应存在时间异质性的情况
简单来说,TWFE 会将早期干预组的干预效应看作“共同的时间趋势”,从而导致晚期干预组的效应估计被严重低估;此问题的处理将放在下文的"TWFE 改进"一章中进行讨论
TWFE 示例
案例说明:
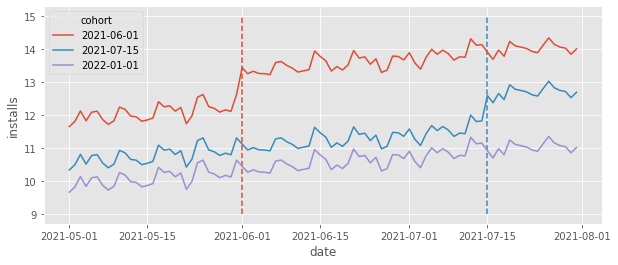
- 目的:评估软件新功能上线对不同城市 APP 安装量的影响
- 上图中三条趋势分别代表三个城市的 APP 安装量;其中红色城市的软件新功能上线时间为 2021-06-01;蓝色城市的软件新功能上线时间为 2021-07-15;紫色城市作为对照组,软件新功能未上线
TWFE 的公式定义如下: $$ Install_{it} = \tau D_{it} + \gamma_i + \theta_t + e_{it} $$
- 其中 $D_{it}$ 表示干预变量,其系数 $\tau$ 对应干预效应的估计;在本案例中,$D_{it}$ 描述了城市 $i$ 在时刻 $t$ 是否上线了新功能;新功能如果已经上线则 $D$ 为 1,否则为 0
- $\gamma_i$ 作为个体固定效应,用来消除个体/组别间的差异;一般是对个体/组别的基准描述(比如城市文化或产品契合度)
- $\theta_t$ 则作为时间固定效应,用来消除时间趋势上的差异;一般每个时间段内都需要统计的外生因素(比如特定时期的基准安装量)
由于虚拟变量过多,因此考虑借助双重机器学习 DML 的思想,对回归模型进行拆分: $$ \begin{align} \tilde{Installs}_{it} &= Installs_{it} - \underbrace{\frac{1}{T}\sum_{t=0}^T Installs_{it}}_\text{Time Average} - \underbrace{\frac{1}{N}\sum_{i=0}^N Installs_{it}}_\text{Unit Average} \\ \ \\ \tilde{D}_{it} &= D_{it} - \frac{1}{T}\sum_{t=0}^T D_{it} - \frac{1}{N}\sum_{i=0}^N D_{it} \end{align} $$ 最后用 $\tilde{Installs}{it} = \tau \tilde D\{it} + e_{it}$ 来快速评估干预效应
TWFE 改进
已知当干预效应存在时间异质性,TWFE 会存在严重的效应估计偏差问题
为了解决这种情况,考虑对 TWFE 的函数形式进行改进,以捕捉时间异质性: $$ Installs_{it} = \sum_{g=0}^G \sum_{t=0}^T \tau_{gt} D_{it} + \gamma_i + \theta_t + e_{it} $$
- 其中 $G$ 表示队列的总数,$g$ 表示一个单独的队列
- 已知每个队列中的效应随着时间推移保持相同的模式
- 通过增加 $T*G$ 个干预效应参数,来捕捉时间异质性
更进一步地思考,干预前的日期效应是可以忽略的,对照组的日期效应也是可以忽略的;因此可以对 TWFE 的函数形式进一步简化,来减少需要处理的参数量: $$ Installs_{it} = \sum_{G=q}^g \sum_{t=g}^T \tau_{gt} D_{it} + \gamma_i + \theta_t + e_{it} $$
- 用条件 $g<q$ 来表示对照组的队列;用条件 $t<g$ 来表示干预前的日期