因果效应评估之准实验
- 通过研究设计(如事件、断点、工具变量)来识别因果
- 利用某种政策变化等机制,模拟出一个近似实验的环境
- 准实验主要用于修正已有数据中不可见的内生性问题
- 准实验不需要满足条件无混杂性,需要满足满足平行趋势假设
配平法的常见算法:双重差分法 DID、工具变量法 IV、面板数据模型、合成控制、断点回归
面板数据模型
面板数据(Panel Data):
- 在多个时期内对同一单元进行重复观测,常见于政策评估/用户追踪
- 面板数据已经控制了所有随时间保持不变的因素(尤其是混杂因素)
- 面板数据只需要评估随时间变化的因素之间的因果关系;比如在分析收入短期增长的原因时,不再需要考虑外貌的这一混杂因素,因为默认外貌在短期内是保持不变的
固定效应:添加个体虚拟变量,来控制个体中不随时间变量的固定变量 (比如外貌或智商)
固定效应模型:$y_{it} = \beta X_{it} + \gamma U_i + e_{it}$
- 其中 $y_{it}$ 表示个体 $i$ 在时间 $t$ 的结果,$X_{it}$ 表示个体 $i$ 在时间 $t$ 的变量向量;$U_i$ 表示个体 $i$ 的一组不可观测变量,这些不可观测变量随时间保持不变,因此没有时间下标; $e_{it}$ 表示误差项。
- 以教育为例,$y_{it}$ 表示工资的对数,$X_{it}$ 表示随时间变化的可观测变量,例如婚姻状况和工作经验,$U_i$ 表示不可观测但对每个个体而言保持不变的变量,例如外貌或智商
时间效应:添加时间虚拟变量,来控制每个时间段内固定不变但可能随时间变化的变量
合成控制法
双重差分法(DID)的平行趋势假设:
- 如果处理组的增长趋势与对照组的趋势不同,DID 就会产生偏差
- 因此在使用双重差分法前,需要检查数据是否满足平行趋势假设
合成控制法(Synthetic Control Method,SCM)
- 通过利用多组数据来合成与控制组趋势相同的数据
- 该方法可以用于修正数据不满足平行趋势假设的问题
- 合成控制作为 DID 的进阶方法,具备更强的适用性
比如当只有一个处理单元(如只有一个省实施了政策)时,可以用其他省份加权合成一个“虚构的省份”来满足假设,并应用双重差分法
以评估加州的禁烟令效应为例:
- 找到其他州的关键特征(GDP、人口和历史香烟销量)
- 利用其他州的关键特征建立回归模型,预测加州的相应数据
- 由此得到不同州的权重,注意确保所有州的权重和为 1
- 利用每个州的权重进行数据组合,得到一个虚构州
- 虚构州作为对照组,用于加州不施行禁烟令下的数据预测
- 对比虚构州和加州在政策实施后的差值,估计禁烟令的因果效应
在估计不同州的权重时,注意避免回归建模出现过拟合的情况
实际应用时,考虑使用 SciPy 包的规划算法来限制权重和为 1
断点回归设计
断点回归设计(Regression Discontinuity Design,RDD)
- 核心思想:比较阈值两侧的结果,从而确定阈值附近的处理效应
- 精确(Sharp RD)断点回归,阈值附近的处理概率从 0 直接跳跃到 1
- 模糊(Fuzzy RD)断点回归,阈值附近的处理概率的变化程度较为平缓
- 断点回归可看作一种局部随机试验,其结果的因果解释性较强(弱于 RCT)
RDD 的算法过程: $$ y_i = \beta_0 + \beta_1 r_i + \beta_2 \mathcal{1}{r_i>c} + \beta_3 \mathcal{1}{r_i>c} r_i $$
- $\beta_{0}$ 表示低于阈值时,回归方程的截距
- $\beta_{0}+\beta_{2}$ 表示高于阈值时,回归方程的截距
- 将断点视作工作变量,则 $\beta_{2}$ 描述了断点的效应
RDD 的示例:
- 思路:利用法定饮酒年龄造成的自然断点,来评估酒精对死亡的影响
- 目的:估算饮酒对 21 岁时各种原因死亡的影响,其结果如下图所示
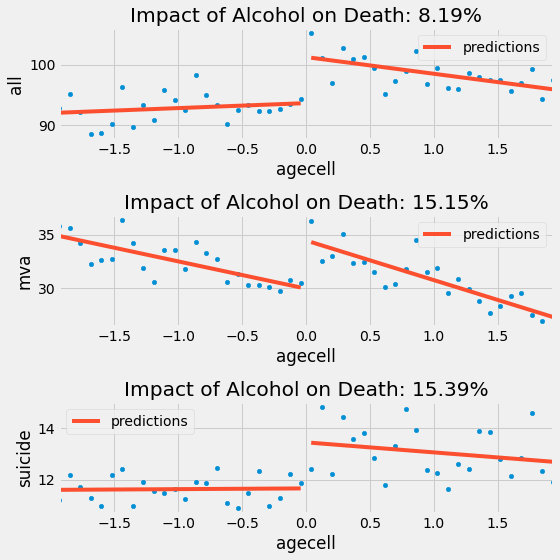
- RDD 结果表明,饮酒会使全因死亡率增加 8.19%,自杀和车祸死亡风险增加 15%
核权重 Kernel Weight:
- 核权重通过提高阈值附近样本的权重,来提高阈值附近的拟合效果
- 最常见的核权重方法是三角核:$K(R, c, h) = \mathcal{1}{|R-c| \leq h} * \left(1-\frac{|R-c|}{h}\right)$
- 其中 $R$ 表示特征,$c$ 表示特征阈值,$h$ 表示带宽,带宽越大,权重的衰减速度越慢
麦克拉里测试 McCrary Test:
- 一种用于验证 RDD 有效性的统计检验方法,是 RDD 的前置
- 数据的“聚集”现象举例:领取政府福利需要收入低于某个特定水平。一些家庭可能会故意降低收入,仅仅是为了刚好符合领取福利的条件,从而导致低于特点收入水平的家庭很多
- 通过麦克拉里测试可以检验是否存在数据的“聚集”问题;麦克拉里测试不通过时,意味着数据的密度曲线在断点附近存在明显跳跃,数据存在“操纵/造假”,此时不能直接使用 RDD