中文标题:LINE:针对大规模信息网络的嵌入表示
英文标题:LINE: Large-scale Information Network Embedding
发布平台:WWW
International Conference on World Wide Web
发布日期:2015-05-18
引用量(非实时):6047
DOI:10.1145/2736277.2741093
作者:Jian Tang, Meng Qu, Mingzhe Wang, Ming Zhang, Jun Yan, Qiaozhu Mei
文章类型:conferencePaper
品读时间:2024-03-19 15:17
1 文章萃取
1.1 核心观点
本文提出了一种称为“LINE”的新型网络嵌入方法,它适用于任意类型的信息网络:无向图、有向图和/或加权图。该方法通过目标函数的优化,同时考虑了网络结构局部和全局信息。此外,本文还提出了一种“边采样”算法,解决了经典随机梯度下降的局限性,提高了推理的有效性和效率。
实验证明了 LINE 在各种现实世界信息网络上的有效性,包括语言网络、社交网络和引文网络。该算法非常高效,能够在常见单机上在几个小时内学习具有数百万个顶点和数十亿条边的网络嵌入表示
1.2 综合评价
- 基于一阶/二阶邻近度作为优化目标,权衡网络的局部和全局信息
- 提出了一种边采样方法,解决梯度爆炸问题的同时改善了训练的效率
- 图领域经典算法,本笔记主要萃取了其中精华部分,对原文有一定取舍
1.3 主观评分:⭐⭐⭐⭐⭐
2 精读笔记
2.1 邻近度的定义
图定义:$G=(V,E)$,其中 $V$ 表示节点的集合,$E$ 表示边的集合
理解一阶/二阶邻近度:
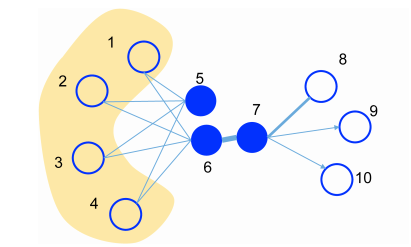
- 节点 6 和节点 7 是直接相连的节点,二者存在一阶临近度
- 节点 5 和节点 6 虽然不直接相连,但存在公共的邻节点(1,2,3,4)
- 因此节点 5 和节点 6 也应该是相似的,即二者存在二阶邻近度
一阶邻近度(First-order Proximity)定义:描述网络中两个顶点之间的局部相似性
- 对于连接节点 $u$ 和节点 $v$ 的边 $(u,v)$,用该边的权重值 $w_{uv}$ 来表示两节点间一阶邻近度
- 如果不存在边 $(u,v)$,则两个节点间的一阶邻近度为 0
- 如果是无权重图,两个直接相连节点之间的一阶邻近度是 1,否则为 0
许多经典的图嵌入算法都以保留一阶邻近性为目标;例如等距特征映射(IsoMap)、1_study/algorithm/数据降维算法/局部线性嵌入 LLE、拉普拉斯特征图和图分解(graph factorization)
二阶邻近度(First-order Proximity)定义:描述网络中两个顶点邻域结构的相似性
- 用 $P_u=(w_{u,1},...,w_{u,|V|})$ 表示节点 $u$ 与其他所有节点之间的一阶临近度
- 则节点 $u$ 和节点 $v$ 之间的临近度由向量 $P_u$ 和向量 $P_v$ 的相似度来定义
- 如果没有节点链接到 $u$ 和 $v$ ,则节点 $u$ 和节点 $v$ 之间的二阶邻近度为 0
本文介绍的 LINE 算法会保留节点的一阶和二阶邻近度
2.2 算法细节
为了建模一阶邻近度,首先定义节点 $i$ 和节点 $j$ 的联合概率分布公式如下: $$ \mathrm{p_1}\left(v_i,v_j\right)=\sigma ({u_i^T}.{u_j})=\frac{1}{1+\exp(-{u_i^T}.{u_j})} $$
- 其中 $u_i$,$u_j$ 分别为节点 $i$ 和节点 $j$ 的 embedding 向量表示
由一阶临近度的定义可知,联合概率分布 $p_1$ 对应的经验分布可定义如下: $$ \hat{p}_{1}(v_i,v_j)=\frac{w_{ij}}{W}=\frac{w_{ij}}{\sum_{(i,j)\in E}w_{ij}} $$
为了保持一阶邻近性,一种直接的方法是最小化两分布的距离(KL 散度): $$ O_1=KL(\hat{p}_1(\cdot,\cdot),p_1(\cdot,\cdot))=-\sum_{(i,j)\in E}w_{ij}\log p_1(v_i,v_j) $$
注意,一阶邻近度仅适用于无向图,不适用于有向图
二阶邻近度适用于有向图和无向图
为了建模二阶邻近度,定义节点 $i$ 和节点 $j$ 的条件概率分布公式如下: $$ p_2(v_j\mid v_i)=\frac{\exp({u}_j^{'T}\cdot{u}_i)}{\sum_{k=1}^{|V|}\exp({u}_k^{'T}\cdot{u}_i)} $$
- 其中 $u_i$,$u_j$ 分别为节点 $i$ 和节点 $j$ 的 embedding 向量表示
- 条件概率分布描述了当节点 $i$ 存在时,节点 $j$ 在节点 $i$ 邻域内的概率
由二阶临近度的定义可知,条件概率分布 $p_2$ 对应的经验分布可定义如下: $$\hat{p}_{2}(v_{j}\mid v_{i})=\frac{w_{ij}}{d_{i}}=\frac{w_{ij}}{\sum_{k\in N(i)}w_{ik}}$$
- 其中 $N(i)$ 表示从节点出发 $i$ 可到达的邻接节点集合
- $d_i$ 描述了节点 $i$ 的出度( out-degree)
为了保持二阶邻近性,最小化两分布的距离(KL 散度): $$ O_{2}=\sum_{i\in V}\lambda_{i}d(\hat{p}_{2}(\cdot\mid v_{i}),p_{2}(\cdot\mid v_{i}))=-\sum_{(i,j)\in E}w_{ij}\log p_{2}(v_{j}\mid v_{i})$$
- 其中 $\lambda_i$ 描述了节点 $i$ 在网络中的重要性;为方便化简,此处定义 $\lambda_i=d_i$
确定两组目标函数后,即可进行 $u_i$,$u_j$ 的调整来寻找最优的节点嵌入表示
以上公式中的两个目标函数($O_1$ 和 $O_2$),最终化简结果均忽略了部分常量
LINE 会根据两个目标函数分别进行单独训练,最终的嵌入表示是二者的拼接
2.3 模型优化
优化 1:负采样降低计算成本
由于计算二阶相似度时,目标函数 $O_2$ 的计算(softmax 函数的分母)需要遍历所有节点;因此为了提高效率,本文借鉴了 word2vec 的负采样优化技巧,最终目标函数变为: $$ \mathrm{log}\sigma({{u}_{n}^{'}}^T\cdot{u}_{i})+\sum_{i=1}^{K}E_{\upsilon_{n}\sim P_{n}(v)}[\mathrm{log}\sigma(-{{u}_{n}^{'}}^T\cdot{u}_{i})] $$
- 其中 $K$ 表示负样本的采样数量;$P_n(v)$ 表示节点 $v$ 被采样的概率
- 一般建议设置 $\mathrm{P_{n}(v)\propto d_{v}^{3/4}}$,其中 $d_v$ 是节点 $v$ 的出度
优化 2:使用异步随机梯度算法(ASGD)+边采样来优化训练
在每次迭代中,设采样的边为 $(i, j)$,节点 $v_i$ 的嵌入向量 $\vec{u}_ {i}$ 所对应的梯度为: $$ \frac{\partial O_2}{\partial{u}_i}=w_{ij}\cdot\frac{\partial\log p_2(v_j|v_i)}{\partial{u}_i} $$
- 注意梯度中包含边权重 $w_{ij}$,而网络中的边权重具有高方差(存在极高/极低的权重值)
- 权重值过高容易导致梯度爆炸,而权重值过低则会影响训练的效率(收敛缓慢)
一种简单粗暴的思路就是将权重为 10 的边看作 10 条权重为 1 的边
而本文则在此思路的基础上,引入了边采样的机制以规避权重值对梯度的影响
本文提出了边抽样的方式以解决边权值的高方差问题:
- 使用异步随机梯度算法(ASGD)来随机选择一批边来更新模型的参数
- 边抽样使用 Alias 采样算法,其中的抽样概率使用边的权重值
- 实际梯度计算时,不再考虑边权值,即梯度计算时的“边权重恒为 1”
- 高权重边的采样概率大,加入梯度更新的次数多,借此利用边权重信息
- 边采样处理在不影响效率的情况下提高了随机梯度下降的有效性
Alias 是一种 $O(1)$ 时间复杂度的离散事件抽样算法
更多细节可参阅 Darts, Dice, and Coins: Sampling from a Discrete Distribution
其他问题 1:如何处理低度节点?
- 此类节点的邻接节点较少,难以合理地推断其节点的嵌入表示
- 考虑利用更高阶(邻居的邻居)的临近度信息来完善权重的评估
$$ w_{ij}=\sum_{k\in N(i)}w_{ik}\frac{w_{kj}}{d_{k}} $$
其他问题 2:如何处理新增节点?
- 若该节点与图中已有节点存在边相连,可考虑冻结参数并单独更新该节点的嵌入表示
- 若该节点与图中已有节点不存在边相连,考虑利用额外的节点信息(未来的工作方向)
2.4 实验分析
实验涵盖了 5 个来自现实世界的网络数据:
| Language Network | Social Network | Social Network | Citation Network | Citation Network | |
|---|---|---|---|---|---|
| Name | Wikipedia | Flickr | Youtube | DBLP(AuthorCitation) | DBLP(PaperCitation) |
| Type | undirected,weighted | undirected,binary | undirected,binary | dircted,weighted | directed,binary |
| |V| | 1,985,098 | 1,715,256 | 1,138,499 | 524,061 | 781,109 |
| |E| | 1,000,924,086 | 22,613,981 | 2,990,443 | 20,580,238 | 4,191,677 |
| Avg. degree | 504.22 | 26.37 | 5.25 | 78.54 | 10.73 |
| labels_num | 7 | 5 | 47 | 7 | 7 |
| train_size | 70,000 | 75,958 | 31,703 | 20,684 | 10,398 |
不同模型的效果对比(简述):
- LINE 方法在不同数据集上表现均超过其他 baseline(DeepWalk 和 SkipGram)
- LINE 方法的训练时长(2.55h)显著低于 DeepWalk(16.64 h),略低于 SkipGram(2.82h)
- 相比于仅使用一阶邻近度,添加二阶邻近度的 LINE 方法性能有明显提高
- 使用边采样方法的 LINE 方法,算法运行效率和最终模型预测性能均有明显提高
模型与网络稀疏性分析:
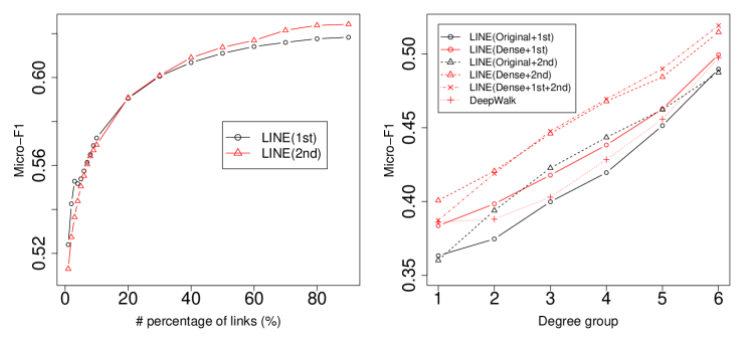
- 二阶邻近度不适用于稀疏网络,但更适用于平均度较低的网络(一阶信息偏少)
- 一阶临近度能补充二阶邻近度在系数网络中的不足,二者有相辅相成的作用
参数的灵敏度分析:
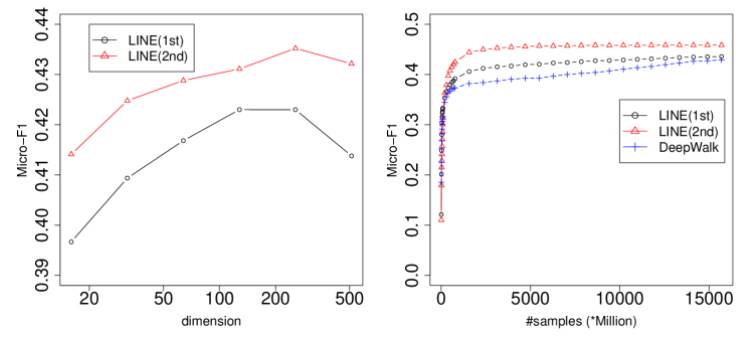
- 随着嵌入表示维度的增加,模型的精度效果会先增加后下降
- 随着训练样本的增加,LINE (2nd)的性能明显更高,并且收敛更快
模型的可拓展性分析:

- 随着线程的增加,模型的训练速度有明显改善,同时最终精度也能保持不变
相关资源
- 论文在线地址
- 开源代码地址
- 本地文件地址:Tang et al_2015_LINE.pdf
- 本地Zotero地址:Tang et al_2015_LINE.pdf