中文标题:语言模型表征空间和时间
英文标题:Language Models Represent Space and Time
发布平台:预印本
发布日期:2023-01-01
引用量(非实时):
DOI:10.48550/ARXIV.2310.02207
作者:Wes Gurnee
DOI:10.48550/ARXIV.2310.02207
作者:Wes Gurnee
循环神经网络(RNNs):具有隐状态、不同层参数共享的神经网络
常见的三种基础 RNNs :RNN、GRU、LSTM
隐变量模型:使用隐状态 $h_{t-1}$ 存储前 $t-1$ 步的序列信息 $$P(x_t|x_{t-1},...,x_1)\approx P(x_t|h_{t-1})$$ $$h_t=f(x_t,h_{t-1})$$ 循环神经网络(recurrent neural networks,RNNs) 是具有隐状态的神经网络
假设时刻 $t$ 的输入为 $X_t \in \mathbb{R}^{n\times d}$,对应的权重参数为 $W
卷积神经网络(CNN):引入了卷积操作的神经网络
严格来说,卷积层是个错误的叫法,因为它所表达的运算其实是互相关运算(cross-correlation)
二维互相关运算示例:
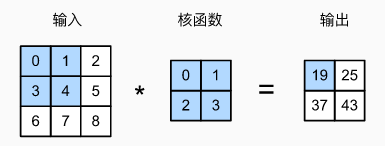
池化(pool)层的优点:降低卷积层对位置的敏感性
常用池化层分两种:最大池化层和平均池化层,前者示例如下:

类似于卷积层,池化层也会有填充和步幅,使用大于 1 的步幅可以起到降维的作用
不同于卷积层,池化层在每个输入通道上是单独计算的,所以池化层的输出通道数等于输入通道数
膨胀(dilated)卷积,也称
柯尼斯堡七桥问题(Seven Bridges of Königsberg)是图论中的著名问题
这个问题是基于一个现实生活中的事例:当时东普鲁士柯尼斯堡(今日俄罗斯加里宁格勒)市区跨普列戈利亚河两岸,河中心有两个小岛。小岛与河的两岸有七条桥连接。在所有桥都只能走一遍的前提下,如何才能把这个地方所有的桥都走遍?

莱昂哈德·欧拉在 1735 年提出,并没有方法能圆满解决这个问题,他更在第二年发表在论文《柯尼斯堡的七桥》中,证明符合条件的走法并不存在,也顺带提出和解决了一笔画问题。
这篇论文在圣彼得堡科学院发表,成为图论史上第一篇重要文献
欧拉把问题的实质归于一笔画问题,即判断一个图是否能够
均值回归:对历史一段时间的值取平均,作为未来每个时刻的预测
指数平滑:预测值是过去一段时间内观测值(或已预测值)的加权平均值
普通回归预测:借助时序相关特征(如节假日、周期性)实现建模预测
更多的时序类衍生特征可参考 1_study/Python/Python 数据处理/tsfresh 时序特征聚合工具
自回归(AR)模型: