分类目录归档：algorithm
支持向量机（support vector machine，简称为SVM）
SVM 算法图解：
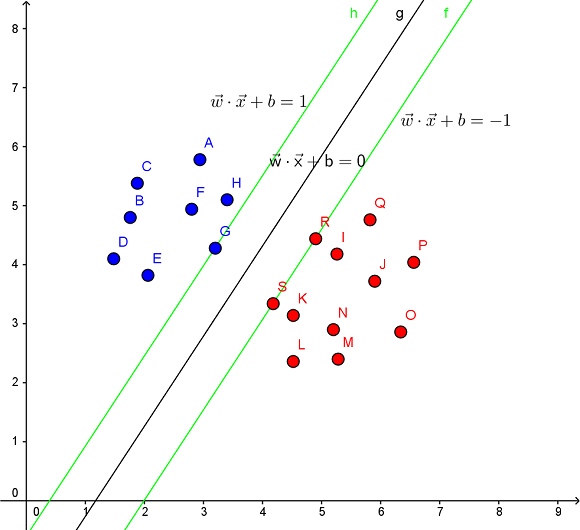
SVM 借助核技巧将输入隐式映射到高维特征空间中，从而有效地进行非线性分类
常见的核函数：
| 核函数 | 表达式 | 备注 |
|---|---|---|
| Linear Kerne |
在统计学中，最小角回归(LARS)是一种将线性回归模型拟合到高维数据的算法
用 $T(\hat{\boldsymbol{\beta}})$ 表示 $\hat{\boldsymbol{\beta}}$ 的绝对值范数 $$T(\hat{\boldsymbol{\beta}})=\sum_{j=1}^m|\hat{\beta_j}|\tag{7}$$ 则Lasso即为下面的约束优化问题： $$\min S(\hat{\boldsymbol{\beta}}) \quad \text{s.t.} \quad T(\hat{\boldsymbol{\beta}}) \le t\tag{8}$$ Las
坐标下降法（英语：coordinate descent）是一种非梯度优化算法。算法在每次迭代中，在当前点处沿一个坐标方向进行一维搜索以求得一个函数的局部极小值。在整个过程中循环使用不同的坐标方向。对于不可拆分的函数而言，算法可能无法在较小的迭代步数中求得最优解。
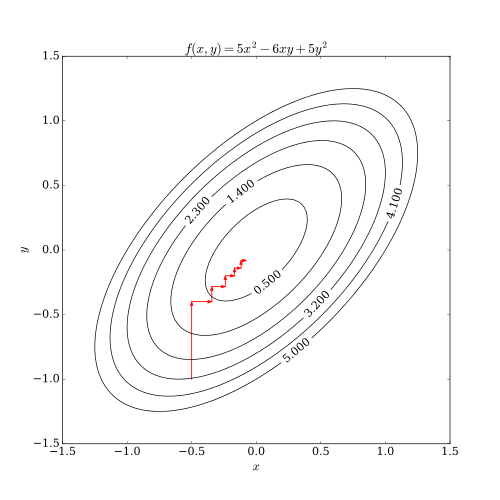
为了加速收敛，可以采用一个适当的坐标系，例如通过主成分分析获得一个坐标间尽可能不相互关联的新坐标系，即自适应坐标下降法。
面对$N$个形式为$(x_i,y_i)$样本组成的样本集，线性回归就是为了寻找形式为$y_{N\times1}=X_{N \times d}\theta_{d\times 1}$的线性方程，使其能最大程度拟合样本，而第一步便是建立线性回归的损失函数/目标函数： $$Loss(\theta)= (y-X\theta)^T(y-X\theta) $$
其中$y$表示真实值，$X\theta$表示的预测值，所以损失函数$Loss(\theta)$表示的便是真实
贝叶斯定理： $$P(B|A)=\frac{P(A,B)}{P(A)}=\frac{P(A|B)P(B)}{P(A)}$$
朴素贝叶斯（Naive Bayes classifier）以贝叶斯定理为基础的简单分类器，主要通过统计历史数据中各种事件的发生频率，并从中寻找统计上的相关性，以实现
粒子群优化（particle swarm optimization，PSO）算法是计算智能领域的一种群体智能的优化算法（其他群体算法举例：蚁群算法，鱼群算法等），该算法最早由Kennedy和Eberhart在1995年提出的，该算法源自对鸟类捕食问题的研究。
鸟类捕食的生物过程：
局部线性嵌入(Locally Linear Embedding，以下简称LLE)是一种重要的降维方法。
和传统的PCA，LDA等关注样本方差的降维方法相比，LLE关注于降维时保持样本局部的线性特征，由于LLE在降维时保持了样本的局部特征，LLE广泛的用于图像图像识别，高维数据可视化等领域。
下图对LLE的原理进行了一个整体描述：
