1 K-means算法概况
K均值算法(即,k-means clustering),是一种无监督聚类算法
K-means算法属于NP-hard问题,不过存在高效的启发式算法,能快速收敛到一个局部最优解
2 K-means算法细节
算法步骤
- 对于N个样本,随机选择其中K个,作为最初的质心
- 遍历所有样本,选择最新的质心进行归类,形成K个簇
- 根据每个簇的样本重新计算质心(比如求均值)
- 重复步骤2-3,直到每个簇质心基本不再变化或达到最大迭代次数
算法的收敛过程如下所示:
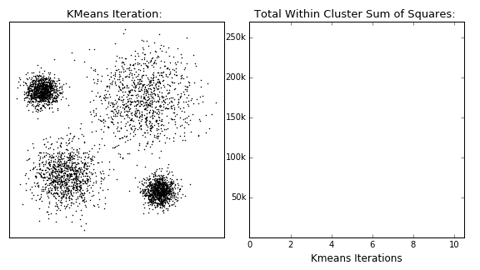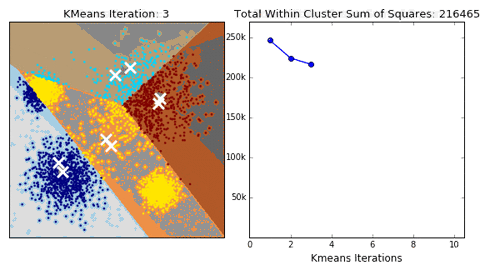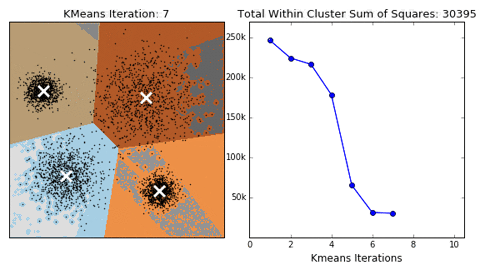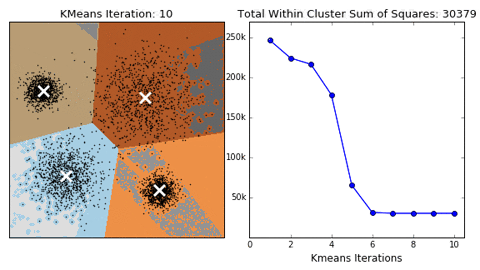 (图源来自https
(图源来自https
分类目录归档:algorithm
K均值算法(即,k-means clustering),是一种无监督聚类算法
K-means算法属于NP-hard问题,不过存在高效的启发式算法,能快速收敛到一个局部最优解
算法步骤
- 对于N个样本,随机选择其中K个,作为最初的质心
- 遍历所有样本,选择最新的质心进行归类,形成K个簇
- 根据每个簇的样本重新计算质心(比如求均值)
- 重复步骤2-3,直到每个簇质心基本不再变化或达到最大迭代次数
算法的收敛过程如下所示:
 (图源来自https
(图源来自https
一个无向图,结点表示随机变量,边表示两个随机变量之间的概率依赖关系,每个随机变量都可以指定一种可能取值,当变量满足马尔可夫性(即变量的可能取值只与它的临近变量有关)时,这时的图就叫马尔可夫网络,也就是马尔可夫随机场。(非严谨定义)
以构建以词性标注为例,假设一个句子由10个单词组成的句子,每个单词的词性选择有10种,则马尔可夫随机场就限制了所有单词的词性只和它前后的单词有关系。
条件随机场
前置知识:1_study/math/马尔可夫模型
可视马尔可夫模型的状态是可知的,而隐马尔可夫模型(The Hidden Markov Model,简称 HMM)的状态是不可知,但存在可知的序列观察值
以典型的看病模型为例,设病人的状态有两种:{健康(Healthy),发烧(Fever)}
医生不能直接知道病人的状态,但能够得知病人的健康状况:{正常(Normal),发寒(Cold), 头晕(Dizzy)},作为一个行医多年的鬼才医生,他可以构建出看病用的隐马尔可夫模型:
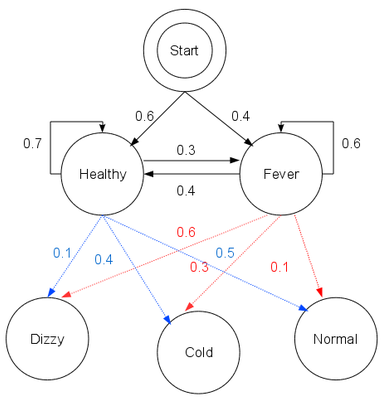
注
概率图模型,在概率模型的基础上,使用基于图的方法来表示概率分布(概率密度/密度函数),是一种通用化的不确定性知识表示和处理方法。
在图模型中,随机变量构成了图中的节点,而随机变量之间的关系(比如相关、独立、不独立、条件独立、因果)则构成了图中节点之间的边
随机变量的常见关系度量指标:
对于随机变量之间的因果关系分析
维特比算法(Viterbi algorithm)是一种寻找最短路径的动态规划算法。可以用于寻找最有可能产生观测事件序列的维特比路径——隐含状态序列,适应于多步骤每步多选择模型的最优选择问题,比如HMM。
维特比算法是针对暴力枚举法的优化
假设有一个长度为$l$的序列,其中$l$对应总天数
其中第$i$天的隐含状态可能情况有$n$种,第$i+1$天的隐含状态可能情况有$m$种
第$i$天的最大概率为$P_i=argmax_k({P_{ik}},k=1,...,n)$,其中$P_{
AC 算法,即 Aho-Corasick 自动机算法,是两位创始人的名称凑出来的(国际惯例起名法了属于是,但是简称和强化学习里的 Actor-Critic 算法重名,需要注意区分~)
此算法的时间复杂度为O(n),与匹配字符串的数目无关,只跟被匹配字符串长度有关
特性:核心思想和[[1_study/algorithm/字符串类算法/单模式匹配算法 KMP]](建议先看懂这个)是一致的,都通过寻找字符串的内部规律,达到每次失配时的高效跳转,只不过AC算使用前缀
KMP,全称为Knuth-Morria-Pratt,是三位创始人的名称凑出来的
KMP 算法是一种字符串匹配算法,时间复杂度 :O(n+m)
特性:字符串头部和尾部会有重复的部分,利用这部分信息,减少匹配次数
理解字符串的前缀和后缀
- 把字符串切割成非空的两份,前面那份就是前缀,后面那份就是后缀
- 所有前缀的可能性组成了前缀集合,所有后缀的可能性组成了后缀集合,比如”Harry”的前缀集合是{”H”, ”Ha”, ”Har”, ”Harr”},而”Potter”的后缀集合是{”otter”,
蒙特卡洛方法(Monte Carlo method),也称统计模拟方法,是二十世纪四十年代中期由于科学技术的发展和电子计算机的发明,而被提出的一种以概率统计理论为指导的一类非常重要的数值计算方法。
蒙特卡洛方法的名字来源于摩纳哥的一个城市蒙特卡洛,该城市以赌博业闻名,而蒙特卡洛方法正是以概率为基础的方法。与它对应的是确定性算法。
蒙特卡洛方法的原理是通过大量随机样本,去了解一个系统,进而得到所要计算的值。
模拟退火算法(Simulated Annealing,SA)的思想最早是由Metropolis等提出的。物理中固体物质的退火过程与一般的组合优化问题之间的相似性,SA是一种由物理退火过程启发的通用优化算法
模拟退火法的物理过程:
遗传算法(Genetic Algorithm, GA)是模拟达尔文生物进化论的自然选择和遗传学机理的生物进化过程的计算模型,是一种通过模拟自然进化过程搜索最优解的方法。
遗传算法的关键要素:
核心过程: