1 瑞利熵函数
瑞利熵(Rayleigh quotient)函数定义如下: $$R(A,x)=\frac{x^HAx}{x^Hx}$$
- 其中$A$为$n\times n$的$Hermitian$矩阵;$x$为非零向量;$H$表示共轭转置
- $Hermitian$矩阵,即厄尔米特矩阵(共轭转置矩阵和自己相等的矩阵)
- 由于现实机器学习中很少遇见复数的情况,因此$A$可考虑为实对称矩阵
瑞利熵$R(A,x)$的重要性质: $$\lambda_{min}\leq R(A,x)\leq \lambda_{max}$$
- 其中$\la
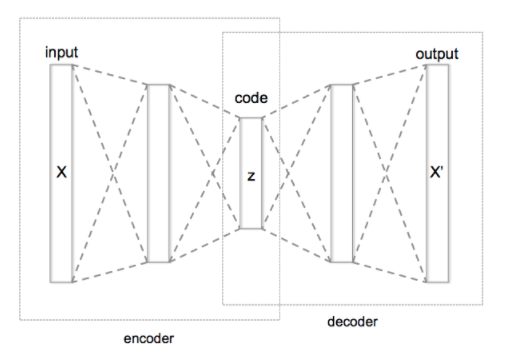 (图源:维基百科-自编码器)
(图源:维基百科-自编码器)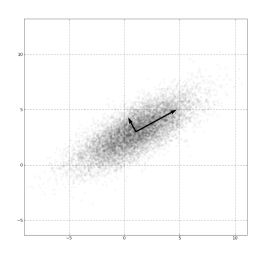 (图源:维基百科-主成分分析)
(图源:维基百科-主成分分析)