分类目录归档：学习
P问题：能在多项式时间内解决的问题，比如快速排序/冒泡排序
NP问题：能在多项式时间内验证得出一个正确解的问题（不确保在多项式时间内找到答案）
NP-Complete（NPC）问题：属于NP问题，其他所有属于NP的问题都可以规约成它
规约（Reduction）：将问题A转化为问题B，使用问题B的解来解问题A
如果问题A可规约为问题B，说明问题B的时间复杂度要大于或等于问题A的时间复杂度，即问题B的难度一般要比问题A大（毕竟B答案能解A，A不一定能解
本文中大部分算法都可通过R语言的latend包复现
轨迹分组算法（Group-based trajectory model，GBTM）
HIS：医院信息系统(Hospital Information System)，为各部门提供病人诊疗/行政管理信息的收集/存储/处理/提取/交换
LIS：实验室信息管理系统(Laboratory Information Management System)，专为医院检验科设计的一套信息管理系统
PACS：医学影像存档与通讯系统(Picture archiving and communication systems)，医学图像的获取/显示/存贮/传送/管理的综合系统
RIS：放射信息管理系统(Radioiogy information system)，是优化医院放射科工作流程管理的软件系统,
首先，理解梯度向量是指向函数值增长最快的方向的：MIT18.02笔记-梯度的定义与理解
定义函数$f(x)$，其在点$x$处沿着方向$d$的变化率可用方向导数表示，即梯度与方向的乘积： $$Df(x;d)=\nabla f(x)^Td$$ 当$d=-\frac{\nabla f(x) }{ ||\nabla f(x)|| }$时，函数$f$在点$x$处的下降速率最大，即负梯度方向为最速下降方向
最速下降算法：在迭代过程，每次都选择负梯度方向搜索（对于寻找最小值的最优化问题）
最速下降算法步骤：
传统傅里叶变换的定义为（积分形式）：$F(\omega)=\mathcal{F}{f(t)}=\int f(t)e^{-i\omega t}dt$
传统逆傅里叶变换的定义为（积分形式）：$f(t)=\mathcal{F}^{-1}{F(\omega)}=\frac{1}{2\pi}\int F(\omega)e^{i\omega t}d\omega$
卷积定理：函数卷积的傅里叶变换是函数傅立叶变换的乘积 $$f\ast g=\mathcal{F}^{
对抗性鲁棒性工具集（Adversarial Robustness Toolbox，ART）是用于机器学习安全性的Python库
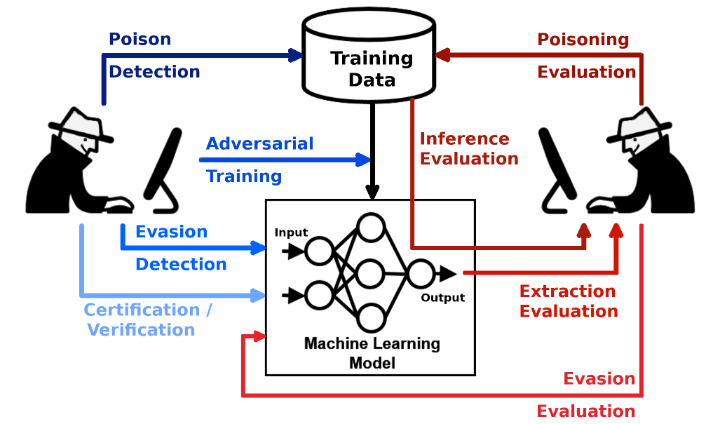
本项目由IBM团队在2019年开源。项目文档不是特别完善，但是示例丰富，API设计
对于回归方程$Y = a + bX + e$，当解释变量$X$和误差项$e$存在相关性时，说明回归模型存在内生性问题
内生性问题的产生原因：
内生性问题的后果：在小样本下，内生变量和外生变量估计系数都有偏。在大样本下，内生变量估计系数不一致。外生变量如果与内生变量不相关，则估计系数一
核密度估计（kernel density estimation，简称KDE）是核平滑对概率密度估计的应用，即一种以核为权重估计随机变量概率密度函数的非参数方法。由Rosenblatt (1955)和Emanuel Parzen(1962)提出，又名Parzen窗（Parzen window）
核密度估计的实现：
$$\hat{f}_h(x)=\frac{1}{n}\Sigma_{i=1}^nK_h(x-x_i)=\frac{1}{nh}\Sigma_