1 图像几何变换
将一幅图像中的坐标位置映射到另一幅图像中的新坐标位置
2D几何变换分类:
- 刚体变换:主要操作包括平移+旋转,变换前后的欧式距离不变,自由度为3
- 相似变换:主要操作包括平移+旋转+缩放,具有保角性,不同点之间的距离比保持不变,自由度为
分类目录归档:学习
将一幅图像中的坐标位置映射到另一幅图像中的新坐标位置
2D几何变换分类:
主成分分析(Principal components analysis,PCA),一种常用的线性降维方法
算法步骤:
图像理解:
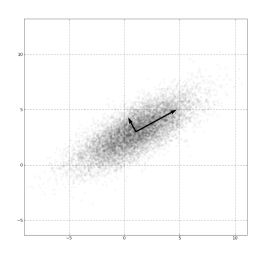 (图源:维基百科-主成分分析)
(图源:维基百科-主成分分析)
PCA 的优缺点分析:
尺度不变特征变换匹配算法(Scale Invariant Feature Transform 简称 SIFT)
SIFT算法常用来提取用于描述影像中的局部性特征,算法主要从空间尺度中寻找极值点,并提取出其位置、尺度、旋转不变量
算法过程:
期望最大化(Expectation-Maximum,简称EM)算法是一种机器学习常见基础算法
EM算法常用于处理存在隐变量的最大似然估计模型,训练过程简单描述如下:
以K-means聚类为例进行直观理解:
EM算法作为一种基础算法,广泛应用于多种算法模型的学习过程,比如:隐马尔可夫模型 HMM
这类算法思想在其他模型中也经常遇见,比
输入重定向:
<:将指定文件的内容作为前面命令的参数
输出重定向:
>:直接把输出覆盖保存到指定文件
>>:把输出尾部追加保存到指定文件
/dev/null
- 类Unix系统中的一个特殊的设备文件
- 作用是像垃圾桶一样接收一切写入其中的数据并丢弃
- 写入操作会提示成功,读取操作会返回一个EOF报错
用于不挂断地运行命令(关闭当前session不会中断程序,只能通过kill等命令删除) 默认情况下该程序的输出都会被重定向到nohup.out文件中,也可以通
本文内容主要摘自:
《Is something better than pandas when the dataset fits the memory?》
代码地址
性能对比主要围绕5个操作展开:
Chinese Whispers(简称CW)算法,是一种无监督的图聚类算法
CW算法运行效率高,但结果存在不确定性,常用于人脸聚类或文本聚类
以人脸聚类为例,先进行图的初始化(构建无向加权图):每个人脸图片为一个节点,不同节点通过计算相似度,然后连接相似度超出指定阈值的节点,并以相似度作为边的权重
算法步骤
- 对于N个人脸样本,每个样本节点先单独成簇(自成一类)
- 遍历所有节点,根据每个节点的邻节点所属类别,计算权重累加
- 修正节点类别,选择最终累加权重最高的类别
- 如果有多个权重最高的类别,
欧氏距离:对应元素求差后计算平方和(要求两个时序长度一致) $$ D(x,y) = \sqrt{(x_1-y_1)^2 + (x_2-y_2)^2 + ... + (x_n-y_n)^2} = \sqrt{\sum\limits_{i=1}^{n}(x_i-y_i)^2} $$ 曼哈顿距离:基于网格地图的路程(比如出租车的行驶路线长度) $$ D(x,y) =|x_1-y_1| + |x_2-y_2| + ... + |x_n-y_n| =\sum\limits_{i=1}^{n}|x_i-y_i| $$ 闵可夫斯基距离