个人笔记

AlpacaEval：主流大语言模型评测

AlpacaEval是一种由斯坦福大小推出的LLM自动评估工具

• 其特点是快速、廉价且可靠
• AlpacaEval 与真实人类注释的一致性很高

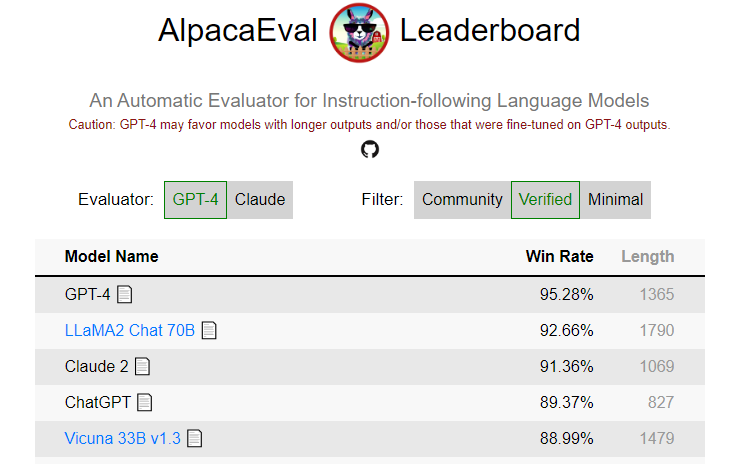
• 2023-09-20 Xwin-LM在 AlpacaEval 上基准测试

Read more

Read more

中文标题：基于知识图谱的约束问答

英文标题：Constraint-Based Question Answering with Knowledge G

Read more

中文标题：SMedBERT_医学语义知识增强型预训练模型

英文标题：SMedBERT

Read more

中文标题：DKPLM_知识增强分解式预训练模型

英文标题：DKPLM: Decomp

Read more

1 基本信息

1.1 书籍名称### 1 什么是 Docker：《动手学深度学习》

1.2 撰写作者：阿斯顿·张，李沐等

1.3 出版日期：在线书籍

1.4 品读时间：2021年12月-2022年8月

1.5 整体耗时：约60h

2 什么是

Read more

中文标题：中文语境的否定与推断意图识别

英文标题：Negation and Speculat

Read more

1 情感分析与数据集

情感分析（sentiment analysis）：研究人们在文本中 （如产品评论、博客评论和论坛讨论等）“隐藏”的情绪

常见应用领域

• 政治（如公众对政策的情绪分析）
• 金融（如市场情绪分析）
• 营销（如产品研究和品牌管理）

情感分析采用的示例数据集是电影评价数据集

基于PyTorch的情感分析数据读取与预处理：

import os
import torch
fr

Read more

1 基本信息

1.1 课程标题：《财务分析与决策》

1.2 授课讲师：清华-肖星

1.3 授课日期：2016 春

1.4 品读时间：初稿成于2016-08，2022-08进行整理复习

1.5 整体耗时：约25h

1.6 摘要

• 了解基本的财务元素及其常见构成（资产、负债表、股东权益）

Read more

本试题内容摘自2016年在 学堂在线 报名的课程《财务分析与决策》，内容可能存在过时

本文内容请勿用于商业用途，对课程有付费意愿的同学可报名最新课程内容

1 单选题（60分）

(60/60 分数)

1、 下列项目中，引起负债有增有减的经济业务是：

• 以银行存款偿还银行借款
• 用银行借款抵付应付账款
• 以银行存款上交税金
• 收到外商捐赠的设备

2

Read more