1 分组机制
按照指定的行列取值进行分组,并按组进行计算(求和、均值、标准差等)
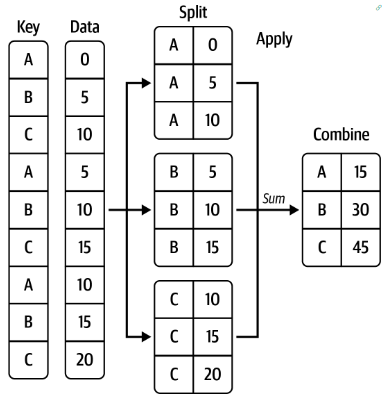
代码示例:
df = pd.DataFrame({'key1' : ['a', 'a', 'b', 'b', 'a'],
'key2' : ['one', 'two', 'o按照指定的行列取值进行分组,并按组进行计算(求和、均值、标准差等)

代码示例:
df = pd.DataFrame({'key1' : ['a', 'a', 'b', 'b', 'a'],
'key2' : ['one', 'two', 'o本章主要围绕matplotlib和seaborn两个模块进行可视化的演示
matplotlib的图像都是基于Figure对象
plt.figure()可以创建一个空白的新Figureadd_subplot创建多子图,并可以依次进行绘制代码示例:
import matp仅搜集收录了部分个人感兴趣的文章,并进行简单记录
2023-02-03 12:29 文章链接
背景知识:
对抗性鲁棒性工具集(Adversarial Robustness Toolbox,ART)是用于机器学习安全性的Python库
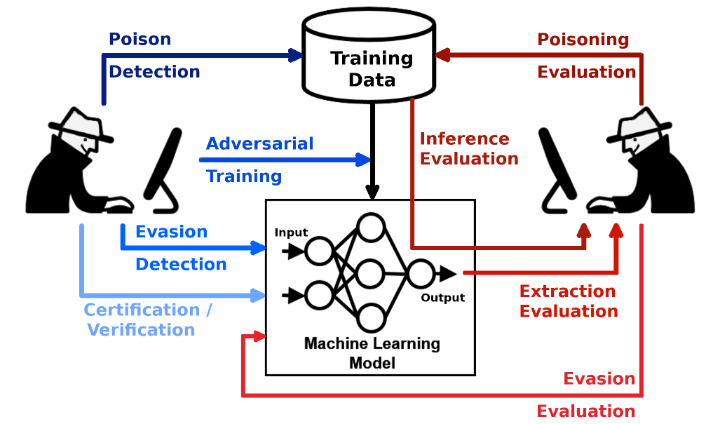
本项目由IBM团队在2019年开源。项目文档不是特别完善,但是示例丰富,API设计
对于回归方程$Y = a + bX + e$,当解释变量$X$和误差项$e$存在相关性时,说明回归模型存在内生性问题
内生性问题的产生原因:
内生性问题的后果:在小样本下,内生变量和外生变量估计系数都有偏。在大样本下,内生变量估计系数不一致。外生变量如果与内生变量不相关,则估计系数一

许立志(1990年7月28日-2014年9月30日),曾用笔名浅晓痕,中国诗人
1990年7月28日,许立志生于广东省揭阳市玉湖镇东寮村。2010年,开始诗歌创作。2011年初,进入深圳富士康工厂成为一名流水线工人。2012年起,在厂刊《富士康人》上发表诗歌、散文等30余篇。2014年9月30日,从深圳龙华一座大厦的17层跳楼身亡,终年24岁。
按照习俗,自杀者不能归葬祖坟。2014年10月15日傍晚,许立志的哥哥将他的骨灰撒进了深圳南澳的海水中。
这大海葬着立志——陈年喜
后来人们