本试题内容摘自2016年在 学堂在线 报名的课程《财务分析与决策》,内容可能存在过时
本文内容请勿用于商业用途,对课程有付费意愿的同学可报名最新课程内容
1 单选题(60分)
(60/60 分数)
1、 下列项目中,引起负债有增有减的经济业务是:
- 以银行存款偿还银行借款
- 用银行借款抵付应付账款
- 以银行存款上交税金
- 收到外商捐赠的设备
2
作者文章归档:王半仙
本试题内容摘自2016年在 学堂在线 报名的课程《财务分析与决策》,内容可能存在过时
本文内容请勿用于商业用途,对课程有付费意愿的同学可报名最新课程内容
(60/60 分数)
1、 下列项目中,引起负债有增有减的经济业务是:
2
企业要赚钱,创造更高的投资回报。
而投资回报决定于效益和效率两个方面:
财务分析的方法如何应用在实际的工作中?
第九周的课程将主要讨论现金流量表(Cash flow statement)的分析
企业在经营、投资、融资活动当中的现金流入流出情况如下图所示:
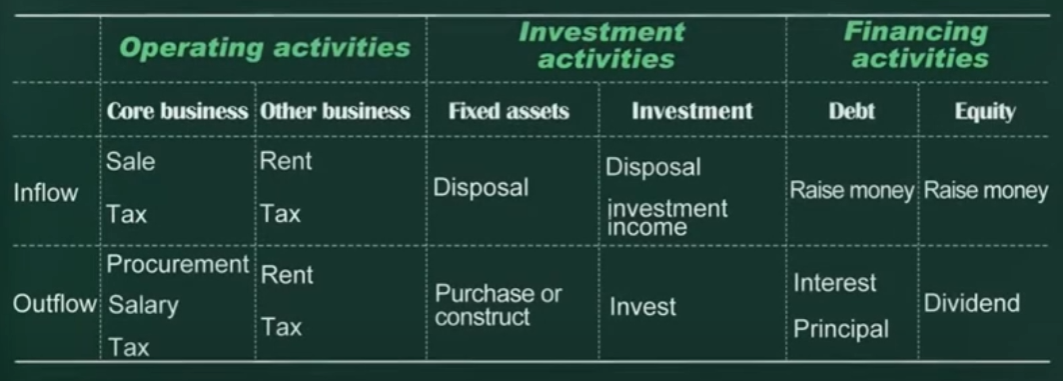
经营、投资、融资活动中的八种可能的现金流状态:
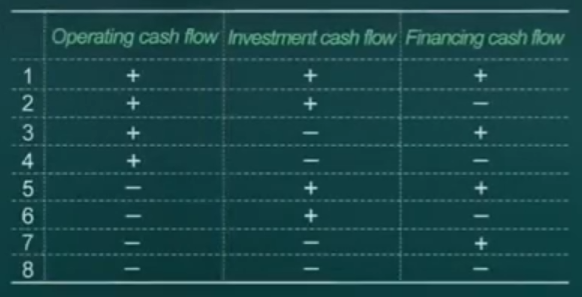 _
_
经营、投资、融资活动中的八种可能的现金流状态,每一种的现金流状态说明:
第1种状态:
Ctrl-Enter : 运行本单元Ctrl-/:注释整行/撤销注释(仅代码状态有效)Tab : 代码补全或缩进Shift-Tab : 提示(输出帮助信息,部分函数、类、方法等会显示其定义原型,如果在其后加 ? 再运行会显示更加详细的帮助)更多快捷键及其说明可参阅5 快捷键
可以自行打开Jupyter Notebook在非编辑模式下,按H键查看所有快捷键
%matplotlib inline # 设定画图结果的自动任意两个不同的 one-hot(独热)向量余弦相似度为0:无法编码词的相似性
两个经典的word2vec模型:skip-gram和CBOW
细节可参阅:1_study/DeepLearning/基础神经网络/词嵌入表示 Embeddings#word2vec
在最优化问题的求解过程中常利用到函数梯度及其高阶信息
牛顿法(Newton's method)又称为牛顿-拉弗森方法(Newton-Raphson method)
牛顿法借助泰勒级数的低阶展开,寻找方程$f(x)=0$的根(因此也被称为切线法)
牛顿法计算步骤:
回顾上一节的核心内容:
好企业的核心在于会”赚钱“,举例说明:
假设某公司的销售收入(营业收入)和净利润的表现如下:
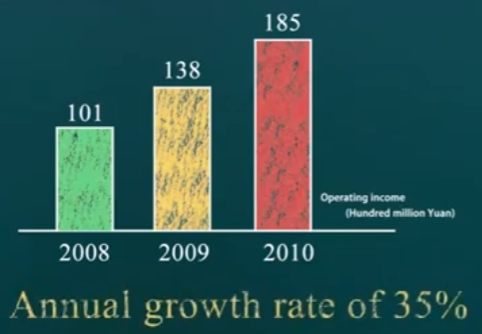
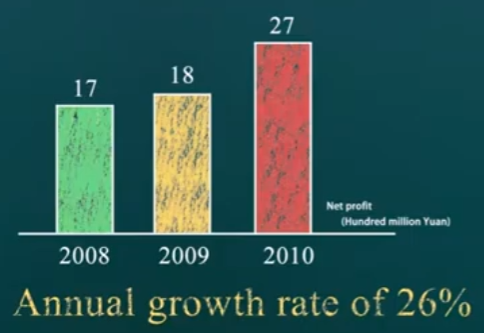
由公式 净利润率=净利润/收入 可知,公司在08年的净利润率约为17%(还不错)
投资资本回报率是描述投资回报的一个指标(用于衡量投出资金
baseline1:使用官方推荐的预训练模型:chinese-bert-wwm-ext 结果:训练最终精度0.8386,略低官方baseline的结果84.4
Training Stop! The best step 2000: 0.8386491557223265
Saving models checkpoint to data/output/qqr/chinese-bert-wwm-ext
baseline2:使用官方推荐的预训练模型:chinese-roberta-wwm-ext-large 结果:训练最终精度0.8393,略低官
公司的盈利能力容易受到决策的影响
所以,综上所述可以归纳出导致企业产生差别的三个层面的因素: