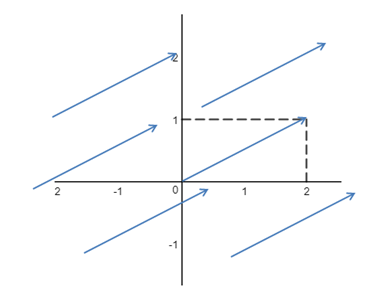
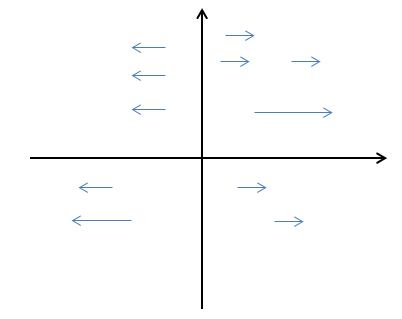
1 通量
通量衡量沿着曲线前进时通过曲线的向量场多少,也可以用于描述单位时间内流体场$\vec{F}$通过曲线$C$的流量: $$∮_c\vec{F}\cdot \hat{n}ds$$
其中$\hat{n}$就是曲线$C$各点处的单位法向量(前进方向的右侧,右正左负是一种约定成俗)
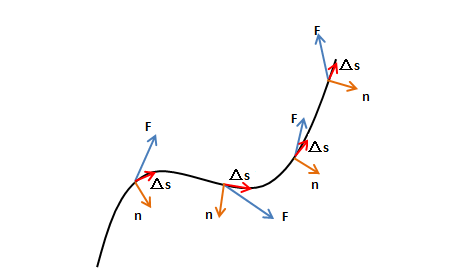
2 通量的简单计算
部分情况下,可根据通量的定义进行直接计算
假设曲线$C$是圆心在原点,半径为$r$的逆时针旋转得到圆
情况1:$\vec{F}//\hat{n}$,可假设$\vec{F}=<x,y>$
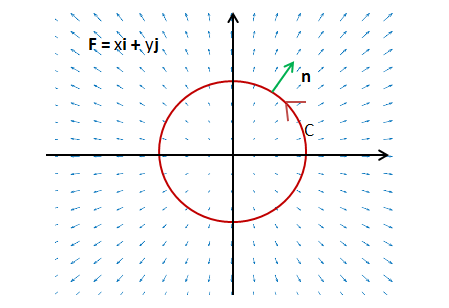 $$∮_
$$∮_