分类目录归档：课程
关于旋度的前置知识可参考之前的21课时中对于旋度的理解
速度场的旋度描述的是速度中的旋转运动分量，也就是角速度
加速度场的旋度描述的是加速度中的旋转运动分量，也就是角加速度
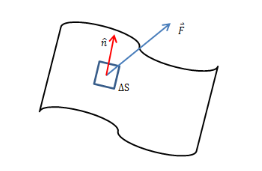
力场的旋度描述的是力的旋转分量，是扭矩力矩与转动惯性的比例，即单位质量的扭转力矩，更具体的来说： $$curl(\frac{力}{质量})=2\frac{扭矩力矩}{转动惯性}$$ 对于保守场$\vec{F}$来说，力来自于势能，而势能会依据能力守恒定律，转化为动能，因此此时的$\vec{F}$不会产生用于旋转的分量，即$curl(\vec{F})=0$
定义单连通区域：区域内的任意一个闭合回路，在该区域内都有一个以它为界的曲面
举例理解：
拓扑学拓展（通过”独立“环路数对曲面进行初步分类）：
- “甜甜圈”形状（doughnut）曲面：横切得到的环路由于内部存在洞所以找不到曲面，竖切得到的环路无法是任何曲面的边界，这两种”独立“环路都不能用于界定曲面边界
- 莫比乌斯环和克莱因瓶：属于不可定向（no-orientable）曲面，比如莫比乌斯环是单侧曲面，所以无法
上一节讲解的扩散方程主要由以下两部分组成：
关于平面线积分的前置知识可参考之前的第19课时的内容
假设在空间向量场$\vec{F}=P\hat{i}+Q\hat{j}+R\hat{k}$的作用下，物体运动轨迹为$c$，则物体的
在上一课时中，对于$\vec{F}=<P,Q,R>$的三维向量场，提出了散度定理： $$∯_S<P,Q,R>\cdot \hat{n}dS=\int \! \! \!\int \! \! \!\int_D (P_x+Q_y+R_z)dV$$
定义三维空间下的$Del$算子：$\nabla=<\partial{}/\partial{x},\partial{}/\partial{y},\partial{}/\partial{z}>$
对于普通三元函数$f$，$\n
前情回顾：
以上的两种示例都属于现实中的特殊情况，本节课程则提出了更为通用的计算方法： $$Flux=\int \! \! \! \int _S\vec{F}\hat{n}dS=\pm \int \! \! \! \int _S\vec{F}\
球坐标系是三维坐标系的一种，以坐标原点为参考点，点$P$的坐标由方位角$\theta$（线$OP$投影到$xy$平面后与$x$轴的夹角）、仰角$\phi$（线$OP$与$z$轴的夹角）和距离$\rho$（点到原点的距离）构成。经纬度就是球坐标系的一种常见形式，其中$\theta$与经度相似，$\phi$与维度相似。
球坐标化通过以下公式实现从$(x,y,z)$到$(\rho,\phi,\theta)$的转化： $$\begin{equation} \left
二重积分的几何意义是面积，三重积分的几何意义是体积，二者的计算也是可以类推的
举例：计算两个曲面$z = x^2+y^2$和$z = 4–x^2–y^2$围成的图形的体积
根据$x^2 + y^2\leq 4 – x^2 – y^2$推得$x,y$的限制条件：$x^2+y^2\leq 2$
将限制条件转化为积分上下限，可得以下计算公式： $$\int \! \! \! \int \! \! \! \int_R fdV=\int_{-\sqrt{2}}^{\sqrt{
单连通区域$R$：由单一的一块组成的区域$R$，即没有“洞”的区域
要求：对于单连通区域$R$内存在的任意闭合曲线$C$，曲线$C$的区域也属于$R$
不满足以上要求的区域则被称为多连通区域，或复连通区域
在之前第21节课中曾提及判定梯度场的前提条件，即$\vec{F}$处处有定义可导。在了解单连通区域的定义后，可以发现此前提条件等价于$\vec{F}$的定义域是单连通区域：
如果$\vec{F}$的旋度是0，且$\vec{F}$的定义域是单连通区域，则$\vec{F}$是保守场/梯度场
