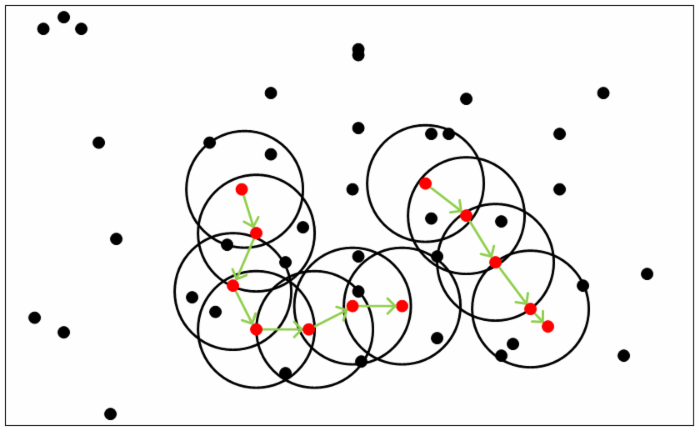
Mean Shift 算法,又称为均值漂移算法
核心思想:
- 该算法假设真实的样本集合是服从不同概率密度分布的数据簇的并集
- 任意选择一个样本通过密度增加最快的方向将收敛到样本密度高的区域
- 样本密度高的区域对应一个分布的聚集区,即样本数据的局部最大值
- 能够收敛到相同局部最大值的样本被认为是服从同一分布的数据簇
算法流程:
- 随机确定样本空间内一个样本 $x$ 作为球心,构建半径为 $h$ 的高维球
$$ S_h\left(x\right)=\left(y\mid\left(y-x\right)\left(y-x\right)^T\leqslant h^2\right) $$ 2. 计算该