作者文章归档：王半仙
Python之禅
The Zen of Python, by Tim Peters
Beautiful is better than ugly. Explicit is better than implicit. Simple is bet
C++、C#、Java、Python
本小节以C++和C#为例，进行了常见面试题的说明和思路介绍，还提供了进阶学习的相关书籍推荐，由于本人C++只学过一点，因此简单记录相关知识点
continuous average： $$lim_{n\to \infty}\frac{y_1+y_2+...+y_n}{n}=\frac{1}{b-a}\int_a^bf(x)dx$$
例题1：单位半圆$y=\sqrt{1-x^2}$的平均高度 $$\frac{1}{1-(-1)}\int_{-1}^1\sqrt{1-x^2}dx=\frac{\pi}{4}$$
例题2：以弧长/角度$\theta$为自变量的单位半圆$y=sin(\theta)$的平均高度 $$\frac{1}{\pi}\int_0^{\pi}sin\t
求半圆函数$(x-a)^2+y^2=a^2$绕$x$轴旋转一周后所形成球的体积$V$
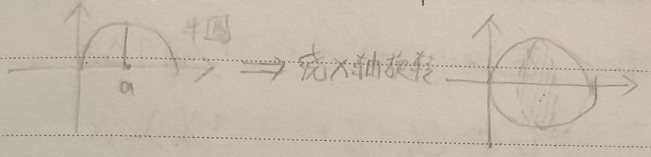
- 半圆函数可化简得$y^2=2ax-x^2$
- 球的每一个切面都是一个圆：$dV=\pi y^2dx$
- 由此可得$V=\int_0^{2a}\pi (2ax-x^2)dx=\frac{4}{3}\pi a^3$
- 球的部分体积满足函数$V(x)=\pi (ax^3-\frac{x^3}{3})$
求函数$y=x^2(y\leq a)$绕$y$轴旋转一周后所形成的物体体
definition of the logarithm： $$L(x)=\int_1^x\frac{1}{t}dt$$
对数函数的性质
- $L'(x)=\frac{1}{x}$与$L(1)=\int_1^1\frac{1}{t}dt=0$，这两个性质唯一的确定对数函数
- 由$L''(x)=-\frac{1}{x^2}$可知，函数处处下凹
- $L'(1)=1$，函数图像在点$(1,0)$位置与$y=x-1$相切
- 函数图像与$y=1$相交于点$(e,1)$，即$e$满足$L(e)=1$
$$\Delta F=Ave(F')\Delta x$$
推导过程
- 由FTC1可知$\Delta F=F(b)-F(a)=F\int_a^bf(x)dx$
- 而$\frac{\Delta F}{\Delta x}=\frac{1}{b-a}\int_a^bf(d)dx=Average(F)$，即$\Delta F=Ave(F')\Delta x$
与中值定理的对比
- 中值定理（MVT）描述的是$\Delta F=F'(c)\Delta x$
- 其中$c$并不确定，只是泛指定
banxian-w.com，费用28￥/年
- 域名实名认证需要先确保腾讯云账号已进行实名认证
- 然后登录腾讯云域名注册控制台并在
我的域名管理页面，选择并点击未实名认证页签，进入实名认证页面- 核对认证域名的信息是，提交相关认证资料以完成认证。
- 认证提交后，没有问题的话，一般会在1个自然日内通过
- 域名实名注册过程参考自腾讯云的域名实名认证说明页面
备案信息需要注意的地方
- 域
Fundamental Theorem of Calculus（FCT1）: $$\text{If }F'(x)=f(x)\text{, then }\int_a^bf(x)dx=F(b)-F(a)=F(x)|_a^b$$
定积分的理解
- 几何解释：积分应该等于函数曲线在X轴以上的面积减去在X轴之下的面积
- 物理解释：思考函数为描述速度$v(t)$，则其原函数$\int_a^b|v(t)|dt$会是描述路程的
$$\int_a^bf(x)dx=F(b)-F(a)$$
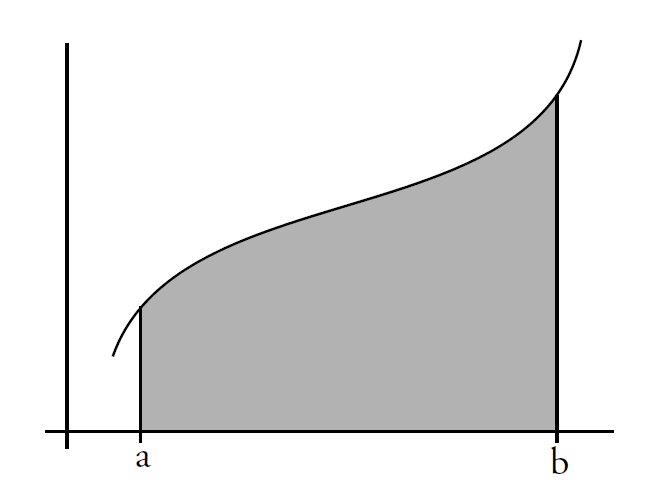
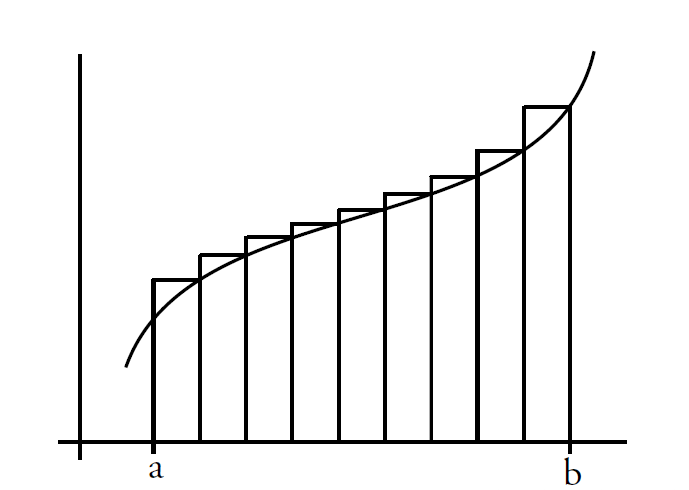
例：计算$y=x^2$从$