Kettle是一款由纯Java语言开发的免费开源的ETL工具
网站链接：https://tianchi.aliyun.com/dataset
天池数据集是阿里集团对外开放的科研数据平台，由阿里巴巴集团业务团队和外部研究机构联合提供，覆盖了电商、娱乐、物流、医疗健康、交通、工业、自然科学、能源等十多个行业，涵盖了数据挖掘、机器学习、计算机视觉、自然语言处理、决策智能等经典的人工智能技术领域。
网站链接：https:/
$$cos^2\theta = \frac{1+cos(2\theta)}{2}$$
$$sin^2\theta = \frac{1-cos(2\theta)}{2}$$
$$\int sin^mxcos^nxdx$$
以上形式的积分，对于任意的$m、n$存在通解
下面将分为两种情况讨论并证明
MinIO是一个用Golang开发的开源分布式对象存储服务
特性：
erasure code和校验和checksum来保护数据免受硬件故障和数据损坏分布式Minio可以让你将多块硬盘（甚至在不同的机器上）组成一个对象存储服务。由于硬盘分布在不同
AWS S3 全名是 Simple Storage Service，简单存储服务。
基本特性：
常用场景：
拉取data_utility下icu分支，命令：
git clone -b icu https://github.com/xingqiuxia/data-utility.git
报错：
Error：RPC failed; result=35, HTTP code = 0
- 原因是git
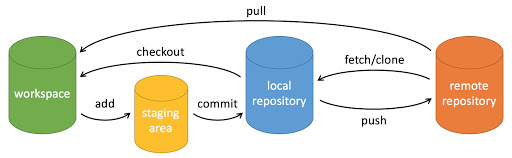
Git 是一个开源的分布式版本控制系统，用于敏捷高效地处理各种项目。
因为传统的集中式版本控制系统（CVS和SVN）不好用，再加上Linux社区不小心跟BitKeeper（为Linux免费提供版本控制服务的供应商）闹翻了，于是Linus直接用C开发了一个分布式版本控制系统，为程序员的世界提供了一片新天地~
# De题目：用数值积分法求解$\int_1^2 \frac{dx}{x}$
先用普通方法计算积分的精确结果（用于精度比较）：
$$\int_1^2 \frac{dx}{x}=lnx|_1^2=ln2\approx0.693147$$
然后使用辛普森公式进行近似值求解：
1）新增
# 创建索引名为 tehero_index 的索引
PUT /tehero_index?pretty
{
# 索引设置
"settings": {
"in