Elasticsearch 是一款开源的全文搜索与分析引擎，它拥有高扩展、大容量数据的存储和处理特性，有着近乎实时的处理效果。elasticsearch 的使用场景还是比较多的，比如 APP 的搜索服务、ELK 实现日志收集与分析、BI 商业智能等。
用于处理没有解析解的积分问题
常见的方法有三种
将区间等长分为n段，然后用矩形去逼近函数
$左和=(y_0+y_1+...+y_{n-1})\Delta x$
$右和=(y_1+y_2+...+y_{n})\Delta x$
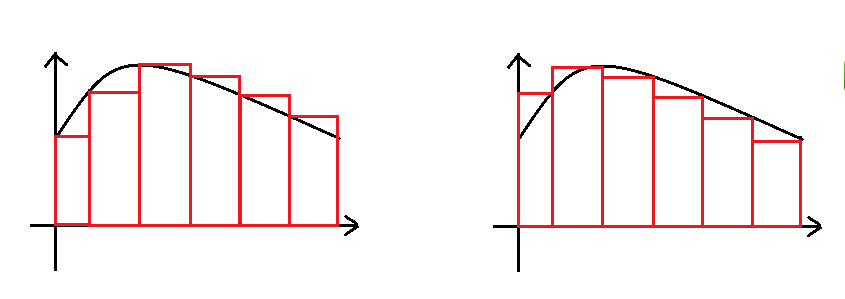
用梯形去逼近函数，精度比黎曼和方法高
$$S=\Delta x(\frac{y_0+y_1}{2}+\frac{y_1+y_2}{2}+..
Syncthing是一款开源免费跨平台的文件同步工具，是基于P2P技术实现设备间的文件同步，所以它的同步是去中心化的，即你并不需要一个服务器，故不需要担心这个中心的服务器给你带来的种种限制，而且类似于torrent协议，参与同步的设备越多，同步的速度越快。
针对隐私问题，Syncthing软件只会将数据存储于个人信任的设备上，不会存储到服务器上。设备之间的通信均通过TLS进行，Syncthing还使用了完全正向保密技术来进一步保障你的数据安全。对于处于不同局域网之中
《解决常见机器学习问题》总结 ⭐⭐⭐⭐
剑指OFFER-总结 未完成
《Docker从入门到实践》总结 ⭐⭐⭐⭐⭐
《动手学深度学习》总结 ⭐⭐⭐⭐
《深度学习500问》总结 ⭐⭐
利用python进行数据分析-总结 ⭐⭐⭐⭐
编写高质量代码改善 Python 程序的 91 个建议-总结 ⭐⭐⭐
经常更新不及时 请见谅
机器学习在预测手术中低血氧的可解释性探究 ⭐⭐⭐⭐⭐
基于多任务训练框架处理标注分歧的问题 ⭐⭐⭐⭐⭐
统计建模的两种文化 ⭐⭐⭐⭐⭐
基于因果框架的医疗领域数据分布偏移评估 ⭐⭐⭐⭐⭐
基于语言模型构建可组合的机器人3D操纵图 ⭐⭐⭐⭐⭐
盘古：基于3D神经网络的中期全球天气准确预测 ⭐⭐⭐⭐⭐
CALM：可信的自适应语言建模 ⭐⭐⭐⭐⭐
ShorT：用于医疗AI公平的捷径学习检测和预防 ⭐⭐⭐⭐⭐
内容全部由Python编码的最佳实践组成，从基本原则、惯用法、语法、库、设计模式、内部机制、开发工具和性能优化8个方